前序遍历迭代算法:
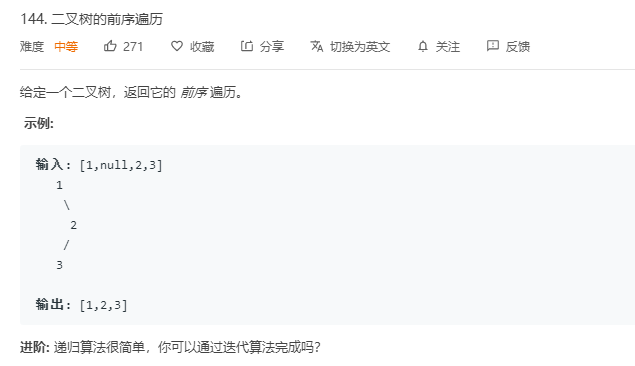
二叉树的前序遍历
二叉树的遍历,整体上看都是好理解的。
三种遍历的迭代写法中,数前序遍历最容易理解。
递归思路:先树根,然后左子树,然后右子树。每棵子树递归。
代码:
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: vector<int> result; vector<int> preorderTraversal(TreeNode* root) { transverse(root); return result; } void transverse(TreeNode*node) { if (node != NULL) { result.push_back(node->val); if(node->left!=NULL) { transverse(node->left); } if(node->right!=NULL) { transverse(node->right); } } } };
2 迭代思路
在迭代算法中,思路演变成,每到一个节点 A,就应该立即访问它。
因为,每棵子树都先访问其根节点。对节点的左右子树来说,也一定是先访问根。
在 A 的两棵子树中,遍历完左子树后,再遍历右子树。
因此,在访问完根节点后,遍历左子树前,要将右子树压入栈。
思路
栈S; p= root; while(p || S不空){ while(p){ 访问p节点; p的右子树入S; p = p的左子树; } p = S栈顶弹出; }
迭代遍历的代码
/** * Definition for a binary tree node. * struct TreeNode { * int val; * TreeNode *left; * TreeNode *right; * TreeNode(int x) : val(x), left(NULL), right(NULL) {} * }; */ class Solution { public: vector<int> result; vector<int> preorderTraversal(TreeNode* root) { stack<TreeNode*>S;//用来存放右子树的节点 TreeNode*Rt = root; while(Rt||S.size()) //根节点不为空 或者 栈中有元素 { while(Rt) //根节点不为空 { result.push_back(Rt->val);//先将Rt节点的访问值保存 S.push(Rt->right); //先保存右子树 Rt = Rt->left;//将指针指向Rt的左子树节点 } Rt = S.top();S.pop(); //当左子树访问完后,紧接着访问右子树,栈顶元素出栈 } return result; } };