Boosting 是一族可将弱学习器提升为强学习器的算法。
关于 Boosting 的两个核心问题:
1.在每一轮如何改变训练数据的权值或概率分布?
通过提高那些在前一轮被弱分类器分错样例的权值,减小前一轮分对样本的权值,而误分的样本在后续受到更多的关注.

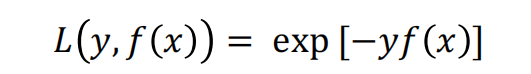
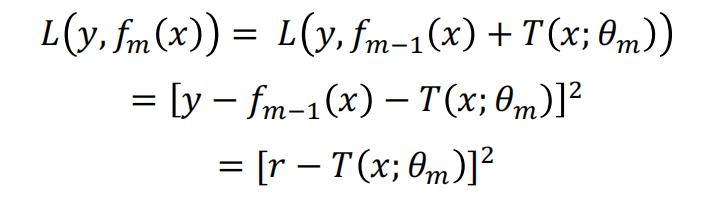 其中r代表的就是残差。
其中r代表的就是残差。



2、通过什么方式来组合弱分类器?
通过加法模型将弱分类器进行线性组合,比如 AdaBoost 通过加权多数表决的方式,即增大错误率小的分类器的权值,同时减小错误率较大的分类器的权值。
而提升树通过拟合残差的方式逐步减小残差,将每一步生成的模型叠加得到最终模型。
常见的 Boosting 算法: AdaBoost,梯度提升决策树 GBDT,XgBoost 以及LightGBM。
一、AdaBoost 算法:
思想:
1、在每轮的迭代中,提高那些前一轮弱分类器分类错误样本的权值,降低那些被正确分类样本的权值,这样一来,那些没有得到正确分类的数据,由于其权值加大后受到后一轮若分类器的更大关注,于是,分类问题被一系列弱分类器分而治之。
2、采用加权多数表决的方法来组合各个弱分类器,具体地说,加大分类误差率小的弱分类器的权值,使其在表决中起到较大的作用,减小分类误差率大的弱分类器的权值,使其在表决中起到较小的作用。
从前向分布算法的思路推到Adaboost:



AdaBoost 算法是前向分步加法算法的特例,这时,模型是由基本分类器组成的加法模型,损失函数是指数函数。 前向分步算法会逐一学习每个基函数,这一过程与 AdaBoost 算法逐一学习基本分类器的过程一致。
AdaBoost 算法的损失函数为指数函数,其形式如下:
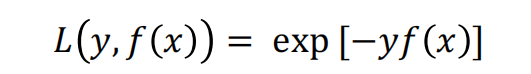
二、梯度提升决策树(GBDT)
1 提升树-boosting tree
以决策树为基函数的提升方法称为ᨀ升树,其决策树可以是分类树或者回归树。提升树模型可以表示为决策树的加法模型。

针对不同的问题的提升树算法主要的区别就在于损失函数的不同,对于回归问题来说,我们使用的是平方损失函数,对于分类问题来说,我们使用的是指数损失函数。对二分类问题来说,提升树算法只需将 AdaBoost 的基分类器设置为二分类树即可,可以说此时的提升树算法时 AdaBoost 算法的一个特例。
对于回归问题的提升树算法来说,我们每一步主要拟合的是前一步的残差,为什么是残差,看下面的公式推导:
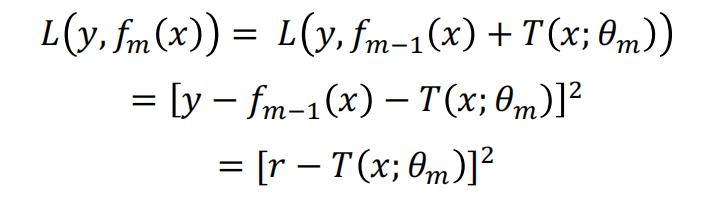 其中r代表的就是残差。
其中r代表的就是残差。回归问题中的提升树算法如下:

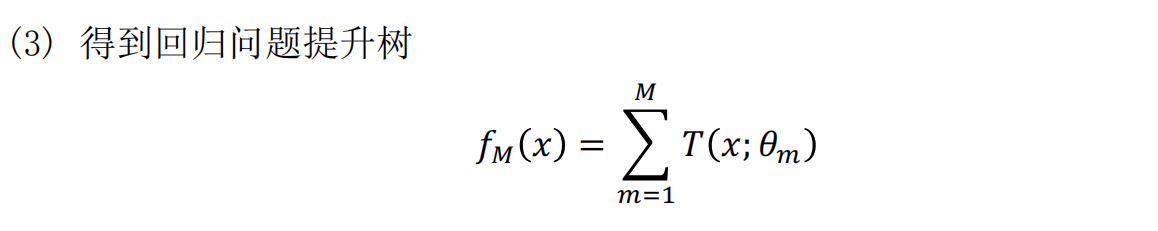
2.梯度提升-Gradient Boosting
梯度提升的思想借鉴于梯度下降法,我们先来回顾一下梯度下降法。对于优化问题:min(f(w)):




基于GBDT 的两个部分,提升树和梯度提升之后,得到GBDT(基模型为cart提升树)的思路为:


