常见的排序算法总结

写在前面：在我们找工作的过程中，经常会被问到是否了解常见的算法，所以，如果想在面试过程中有个良好的表现，对常见的排序算法有一定的了解是必须的。

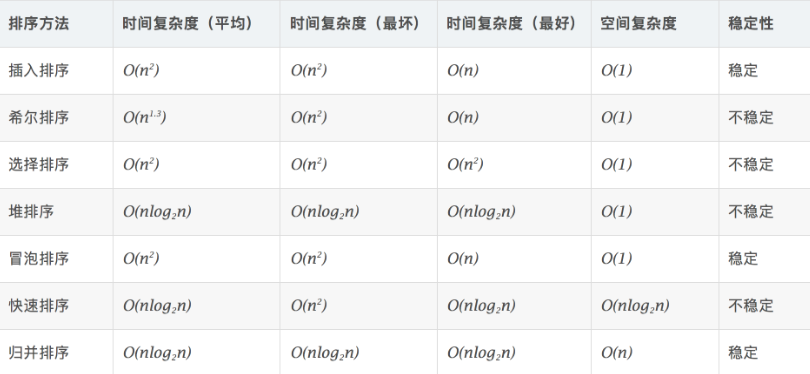
七种常见排序算法总结

第一类：交换排序

1、冒泡排序

原理说明：

（1）比较相邻的元素，如果第一个比第二个大，就交换它们两个；

（2）对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数；

（3）针对所有的元素重复以上的步骤，除了最后一个；

（4）重复步骤1~3，直到排序完成。

代码实现：

#include <stdio.h>

int main()
{
    int A[]={6,5,3,1,8,7,2,4};
    int n=sizeof(A)/sizeof(int);
    //从小到大
    int tmp=0;
    for(int i=0;i<n-1;i++)
    {
        for(int j=0;j<n-1-i;j++)
        {
            if(A[j]>A[j+1])
            {
                tmp=A[j];
                A[j]=A[j+1];
                A[j+1]=tmp;
            }
        }
    }
    for(int i=0;i<n;i++)
    {
        printf("%d ",A[i]);
    }
    return 0;
}

2、快速排序

原理说明：

（1）从序列中挑出一个元素，作为"基准"；

（2）把所有比基准值小的元素放在基准前面，所有比基准值大的元素放在基准的后面（相同的数可以到任一边），这个称为分区操作；

（3）对每个分区递归地进行步骤1~2，递归的结束条件是序列的大小是0或1，这时整体已经被排好序了。

代码实现：

#include <stdio.h>

int part(int *A,int left,int right)
{
    int pivot=left;
    int index=left+1;
    int tmp=0;
    for(int i=index;i<=right;i++)
    {
        if(A[i]<A[pivot])
        {
            tmp=A[i];
            A[i]=A[index];
            A[index]=tmp;
            ++index;
        }
    }
    tmp=A[pivot];
    A[pivot]=A[index-1];
    A[index-1]=tmp;
    return index-1;
}

void quickSort(int *A,int left,int right)
{
    int pivotIndex;
    if(left<right)
    {
        pivotIndex=part(A,left,right);
        quickSort(A,left,pivotIndex-1);
        quickSort(A,pivotIndex+1,right);
    }
}

int main()
{
    int A[]={5,2,9,4,7,6,1,3,8};
    int n=sizeof(A)/sizeof(int);
    quickSort(A,0,n-1);
    for(int i=0;i<n;i++)
    {
        printf("%d ",A[i]);
    }
    return 0;
}

第二类：插入排序

1、简单插入排序

原理说明：

（1）从第一个元素开始，该元素可以认为已经被排序；

（2）取出下一个元素，在已经排序的元素序列中从后向前扫描；

（3）如果该元素（已排序）大于新元素，将该元素移到下一位置；

（4）重复步骤3，直到找到已排序的元素小于或者等于新元素的位置；

（5）将新元素插入到该位置后；

（6）重复步骤2~5。

代码实现：

#include <stdio.h>

int main()
{
    int A[]={6,5,3,1,8,7,2,4};
    int n=sizeof(A)/sizeof(int);
    //从小到大
    int i,j,tmp;
    for(i=1;i<n;i++)
    {
        tmp=A[i];
        for(j=i-1;j>=0 && tmp<A[j];j--)
        {
            A[j+1]=A[j];
        }
        A[j+1]=tmp;
    }
    for(i=0;i<n;i++)
    {
        printf("%d ", A[i]);
    }
    return 0;
}

2、希尔排序

原理说明：

（1）插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率；

（2）插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位。

代码实现：

#include <stdio.h>

void shellSort(int *A,int n)
{
    int step=n/2;
    int i,j,tmp;
    while(step>=1)
    {
        for(i=step;i<n;i++)
        {
            tmp=A[i];
            for(j=i-step;j>=0 && A[j]>tmp;j-=step)
            {
                A[j+step]=A[j];
            }
            A[j+step]=tmp;
        }
        step/=2;
    }
}

int main()
{
    int A[]={6,5,3,1,8,7,2,4};
    int n=sizeof(A)/sizeof(int);
    shellSort(A,n);
    for(int i=0;i<n;i++)
    {
        printf("%d ",A[i]);
    }
    return 0;
}

第三类：选择排序

1、简单选择排序

原理说明：

（1）初始时在序列中找到最小（大）元素，放到序列的起始位置作为已排序序列；

（2）再从剩余未排序元素中继续寻找最小（大）元素，放到已排序序列的末尾；

（3）以此类推，直到所有元素均排序完毕。

代码实现：

#include <stdio.h>

int main()
{
    int A[]={6,5,3,1,8,7,2,4};
    int n=sizeof(A)/sizeof(int);
    //从小到大
    int index,tmp;
    for(int i=0;i<n-1;i++)
    {
        index=i;
        for(int j=i+1;j<n;j++)
        {
            if(A[j]<A[index])
            {
                index=j;
            }
        }
        tmp=A[i];
        A[i]=A[index];
        A[index]=tmp;
    }
    for(int i=0;i<n;i++)
    {
        printf("%d ",A[i]);
    }
    return 0;
}

2、堆排序

原理说明：

堆排序是指利用堆这种数据结构所设计的一种选择排序算法，堆是一种近似完全二叉树的结构。

（1）由输入的无序数组构造一个最大堆，作为初始的无序区；

（2）把堆顶元素（最大值）和堆尾元素互换；

（3）把堆（无序区）的尺寸缩小1，并从新的堆顶元素开始进行堆调整；

（4）重复步骤2，直到堆的尺寸为1。

代码实现：

#include <stdio.h>

//堆调整
void heapAdjust(int *A,int i,int size)
{
    int leftChild=2*i+1;
    int rightChild=2*i+2;
    int root=i;
    if(leftChild<size && A[leftChild]>A[root])
    {
        root=leftChild;
    }
    if(rightChild<size && A[rightChild]>A[root])
    {
        root=rightChild;
    }
    int tmp;
    if(root!=i)
    {
        tmp=A[i];
        A[i]=A[root];
        A[root]=tmp;
        heapAdjust(A,root,size);
    }
}

void heapSort(int *A,int size)
{
    //建立堆
    for(int i=size/2-1;i>=0;i--)
    {
        heapAdjust(A,i,size);
    }
    int tmp;
    for(int i=size-1;i>0;i--)
    {
        tmp=A[0];
        A[0]=A[i];
        A[i]=tmp;
        heapAdjust(A,0,i);
    }
}

int main()
{
    int A[]={6,5,3,1,8,7,2,4};
    int n=sizeof(A)/sizeof(int);
    heapSort(A,n);
    for(int i=0;i<n;i++)
    {
        printf("%d ",A[i]);
    }
    return 0;
}

第四类：归并排序

1、二路归并排序

原理说明：

递归实现的归并排序是算法设计中分治策略的典型应用，我们将一个大问题分割成小问题分别解决，然后用所有小问题的答案来解决整个大问题。

（1）申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；

（2）设定两个指针，最初位置分别为两个已经排序序列的起始位置；

（3）比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；

（4）重复步骤3直到某一指针到达序列尾；

（5）将另一序列剩下的所有元素直接复制到合并序列尾。

代码实现：

#include <stdio.h>
#include <stdlib.h>

//合并两个已排好序的数组
void merge(int *A,int left,int mid,int right)
{
    int len=right-left+1;
    int *tmp=(int*)malloc(sizeof(int)*len);
    int i=left;
    int j=mid+1;
    int index=0;
    while(i<=mid && j<=right)
    {
        tmp[index++]=A[i]<=A[j]?A[i++]:A[j++];
    }
    while(i<=mid)
    {
        tmp[index++]=A[i++];
    }
    while(j<=right)
    {
        tmp[index++]=A[j++];
    }
    for(int k=0;k<len;k++)
    {
        A[left++]=tmp[k];
    }
    free(tmp);
}

void mergeSort(int *A,int left,int right)
{
    int mid;
    if(left<right)
    {
        mid=(left+right)/2;
        mergeSort(A,left,mid);
        mergeSort(A,mid+1,right);
        merge(A,left,mid,right);
    }
}

int main()
{
    int A[]={6,5,3,1,8,7,2,4};
    int n=sizeof(A)/sizeof(int);
    mergeSort(A,0,n-1);
    for(int i=0;i<n;i++)
    {
        printf("%d ",A[i]);
    }
    return 0;
}

附：在我们做笔试的过程中，经常会用到全排与组排的算法思想，所以在这里也一并的整理出来。

1、全排算法

代码实现：

#include<stdio.h>
#include <stdlib.h>

void swap(int *p1,int *p2)
{
    int t=*p1;
    *p1=*p2;
    *p2=t;
}

void permutation(int a[],int index,int size)
{
    if(index==size)
    {
        for(int i=0;i<size;i++)
            printf("%d ",a[i]);
        printf("
");
    }
    else
    {
        for(int j=index;j<size;j++)
        {
            swap(&a[j],&a[index]);
            permutation(a,index+1,size);//此处用到递归思想
            swap(&a[j],&a[index]);
        }
    }
}

int main()
{
    int n;
    scanf("%d",&n);
    int *a=(int*)malloc(sizeof(int)*n);
    for(int i=0;i<n;i++)
        a[i]=i+1;
    permutation(a,0,n);
    free(a);
    return 0;
}

输入：

4

输出：

1 2 3 4
1 2 4 3
1 3 2 4
1 3 4 2
1 4 3 2
1 4 2 3
2 1 3 4
2 1 4 3
2 3 1 4
2 3 4 1
2 4 3 1
2 4 1 3
3 2 1 4
3 2 4 1
3 1 2 4
3 1 4 2
3 4 1 2
3 4 2 1
4 2 3 1
4 2 1 3
4 3 2 1
4 3 1 2
4 1 3 2
4 1 2 3

2、组排算法

代码实现：

#include<stdio.h>
#include <stdlib.h>

void combine(int n,int m,int a[],int b[],const int M)
{
    for(int j=n;j>=m;j--)
    {
        b[m-1]=j-1;
        if(m>1)combine(j-1,m-1,a,b,M);//用到了递归思想
        else
        {
            for(int i=M-1;i>=0;i--)
            {
                printf("%d ",a[b[i]]);
            }
            printf("
");
        }
    }
}

int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    int *a=(int*)malloc(sizeof(int)*n);
    int *b=(int*)malloc(sizeof(int)*m);
    for(int i=0;i<n;i++)
        a[i]=i+1;
    const int M=m;
    combine(n,m,a,b,M);
    free(a);
    free(b);
    return 0;
}

输入：

4 3

输出：

4 3 2
4 3 1
4 2 1
3 2 1

后记：欢迎各路大神批评与指正！