数据备份

147. 数据备份

算法进阶上的题是真的毒瘤..

知到打完(抄题解)代码,才貌似理解了一丢丢....惭愧...

让我们重新理一下思路,这种题就是看到题,不会思路,会思路不会写的题目,所以我们要慢慢来...

首先我们需要搞点性质...第一直觉,最短的距离和,应该不会有跨过某个点去找其他的点吧,因为如果存在这样的方案,显然与周围的点配对要更优...于是乎我们知道一个点如果要对答案产生贡献,必然是与周围的点配对的..

可是这简陋的性质,好像不能支撑我们做这个题目...没办法,继续挖掘性质...

这里就直接将结论放上去了：如果存在一个区间,去建立的每个点都是与周围点配对,如果再多选一条边,如果最优解要破坏其中的情况,那么必然吗是全部破坏的...

见图：我们要选择虚线的话,也就是要破坏实线,最优解一定满足虚线全部选..

首先当我们k==2的情况,（k==1我们直接选最小的边即可）.

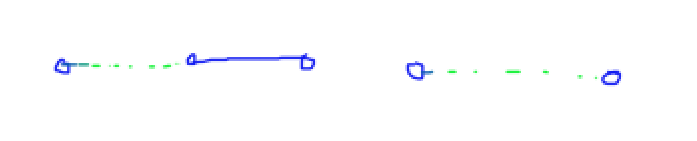
图中蓝色实线为我们k==1的选择,如果此时k==2最优解绿色,即我们破坏了实线,但却选择了并非相邻的区域,我们看看是否有什么矛盾.由于蓝色线咸鱼绿色线,所以我们选择蓝线与右边的绿线一定由于现在两条绿线的选择,所以绿色的线为最优解矛盾.

之后我们直接拓展到k的情况,即知道了k-1的最优解为连续的情况,看结论是否任然成立.

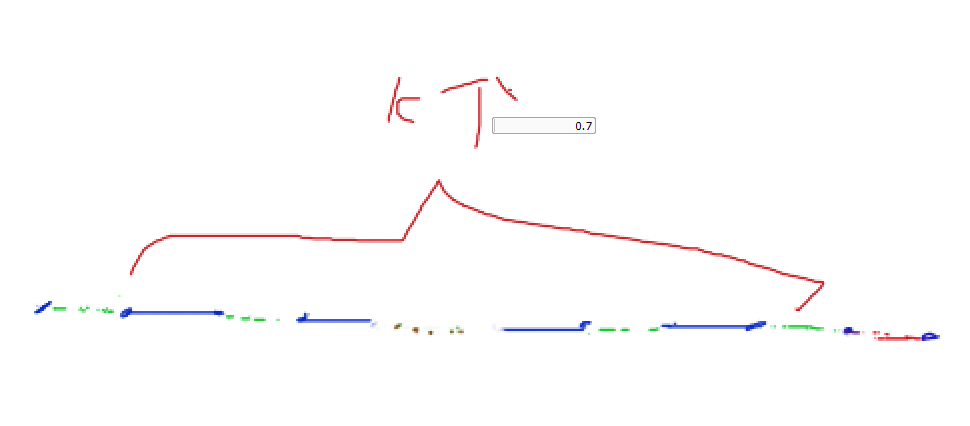
我们看蓝色为上一个的最优解,绿线是应该到达的轨迹.如果我们假设最优解不是这,也就是起码有一条绿线跑去其他的位置了，如图中红色线的位置.我们发现红线和蓝线,绿线没有交集,也就是说红线可以加到绿线和蓝线的任一个集合中.

而此时比较蓝线和绿线,由于蓝线是上一次的最优解,所以在抛去红线的k-1个绿线的权值大于蓝线，而此时的最优解显然是蓝线+红线，与绿线是最优解矛盾..

此时我们又发现一个性质,即如果再一段连续的线中,要么选择与他毫不相及的边,如果选的边有交集,那一定是将原本的连续得全部破坏才有可能是最优解...

那们我们就可以做这道题了,首先我们将边化点,点权为相邻边的距离.

之后我们思考要用到的数据结构,我们要在当前选择一个最优决策,然后修改状态,加入下一个决策.用set和堆都行...

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=100010;
int n,k,l[N],r[N];
ll s[N];
set<pair<ll,int> >se;
set<pair<ll,int> >::iterator it;
inline void del(int p)
{
    r[l[p]]=r[p];
    l[r[p]]=l[p];
}
int main()
{
    cin>>n>>k;
    for(int i=0;i<n;++i) cin>>s[i];
    for(int i=n-1;i>=1;--i) s[i]-=s[i-1];
    s[0]=s[n]=1e15;
   for(int i=0;i<=n;++i)
   {
       l[i]=i-1;
       r[i]=i+1;
       if(i>=1&&i<n) se.insert({s[i],i}); 
   }
   ll ans=0;
   while(k--)
   {
       it=se.begin();
       ll v=it->first;
       int p=it->second;int left=l[p],right=r[p];
       del(left);del(right);
       se.erase(it);se.erase({s[left],left});se.erase({s[right],right});
       s[p]=s[left]+s[right]-s[p];
       se.insert({s[p],p});
       ans+=v;
       
   }
   printf("%lld",ans);
   return 0;
}