kruskal是最小生成树的一种做法,即严格按照贪心思想将边从小到大排序,一个一个枚举能不能加入图中,知道生成一棵树,显然树为最小树。
鄙人觉得kruskal做法远不止如此,那种严格从小到大选边的做法还有大用途...
例题:

此题也是生成一棵树,只不过生成一颗树边的最大值减最小值最小的树。那就有点难办...
这是我们就可以从题目要找的树本身入手思考,题目要求的树中有最大边与最小边,假设我们知道最小边,我们就可以用贪心的思想依次选择比最小边大但离最小值最近的边看是否能加入图中.即以最小边为基准找边。可是连最小边也不知道,怎么办?只能枚举了,即枚举每一条边当做基准,依次将比它大的边判断后入图,这就用到kruskal了,先按边小到大排序,依次枚举每一个边当基准,向后找生成树,更新找到的最小边差。
#include<bits/stdc++.h> using namespace std; int n,m,f[1000],tot,pd,cnt; struct bian { int x,y,v; }; bian a[100000]; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') ff=-1; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*ff; } int getf(int k) { if(k==f[k]) return k; else return (f[k]=getf(f[k])); } bool paixu(bian x,bian y) { return (x.v<y.v); } inline void work1() { for(int i=1;i<=n;i++) f[i]=i; for(int i=1;i<=tot;i++) { int x=getf(a[i].x); int y=getf(a[i].y); if(x!=y) f[x]=y; } int ans=getf(1); for(int i=1;i<=n;i++) { if(getf(i)!=ans) { pd=1; break; } } } inline void work2() { sort(a+1,a+1+tot,paixu); int minn=654646545; for(int i=1;i<=tot-n+2;i++) { int ans=-156465454,cnt=0,b=a[i].v; for(int k=1;k<=n;k++) f[k]=k; for(int j=i;j<=tot;j++) { int x=getf(a[j].x); int y=getf(a[j].y); if(x!=y) { ans=max(ans,a[j].v-b);f[x]=y; if(++cnt==n-1) break; } } //cout<<minn<<endl; if(cnt==n-1) minn=min(minn,ans); } cout<<minn<<endl; } int main() { //freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=m;i++) { int x=read(),y=read(),v=read(); a[++tot].x=x; a[tot].y=y; a[tot].v=v; } work1(); if(pd==1) {cout<<-1<<endl;return 0;} work2(); return 0; }
这启示我们遇到边权差最小的树时可用kruskal解决.
下一题:

此题同样求最小边权差,只不过从特定的一点到另一点,不是全图的最小边权差.
怎么办呢?还从题目要求的情况考虑:从起点到终点是一个连通区域,我们用kruskal不断加边时,加入一个边就可以判断起点与终点是否连通,如果连通就没有继续加边的必要了,同时由于提前排好序的缘故,最后加的边一定是图中的最大边,且一定在从起点到终点的路径上(很显然,因为起点到终点是在加了此边才连通,没加之前起点与终点各是一个区域,而此边就是联通两个区域的唯一边,所以一定在路径上),
最大边找到了,剩下的就是最小边了,同样我们可以用枚举每条边当做基准,可是这又有问题,生成的图中,最小边可能不在路径内,如下图:
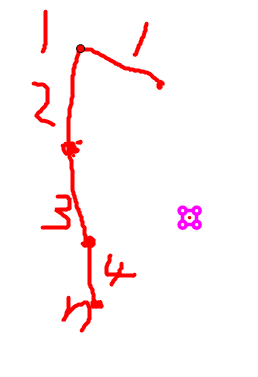
最小边为1,以1为基准可1不在路径中,算出的答案自然比正答大,可是如果1不在路径中,等到我们用2为基准时一定会遍历到这种情况,此时算出的答案就是正解了,可见这种解法并没有错。
代码:
#include<bits/stdc++.h> using namespace std; const int maxn=1100; int n,m,T,f[maxn]; struct bian { int x,y,v; }; bian a[maxn]; inline int read() { int x=0,ff=1; char ch=getchar(); while(!isdigit(ch)) { if(ch=='-') ff=-1; ch=getchar(); } while(isdigit(ch)) { x=(x<<1)+(x<<3)+(ch^48); ch=getchar(); } return x*ff; } inline void put(int x) { if(x<0) putchar('-'),x=-x; if(x>9) put(x/10); putchar(x%10+'0'); } inline bool paixu(bian x,bian y) { return (x.v<y.v); } int getf(int x) { if(f[x]==x) return x; else return(f[x]=getf(f[x])); } inline bool check(int qi,int zh) { for(int i=1;i<=n;i++) f[i]=i; for(int i=1;i<=m;i++) { int t1=getf(a[i].x); int t2=getf(a[i].y); if(t1!=t2) f[t1]=t2; } if(getf(qi)==getf(zh)) return true; else return false; } inline int work(int qi,int zh) { int minn=0,maxx=0,ans=INT_MAX; for(int i=1;i<=m;i++) { minn=a[i].v;maxx=0; for(int i=1;i<=n;i++) f[i]=i; for(int j=i;j<=m;j++) { int t1=getf(a[j].x); int t2=getf(a[j].y); if(t1!=t2) { f[t1]=t2; if(getf(qi)==getf(zh)) { maxx=a[j].v; break; } } } if(maxx) ans=min(ans,maxx-minn); } return ans; } int main() { freopen("1.in","r",stdin); n=read();m=read(); for(int i=1;i<=m;i++) { a[i].x=read(); a[i].y=read(); a[i].v=read(); } sort(a+1,a+1+m,paixu); T=read(); for(int i=1;i<=T;i++) { int qi=read(),zh=read(); if(check(qi,zh)) put(work(qi,zh)),cout<<endl; else put(32475),cout<<endl; } return 0; }
好了,kruskal就说到这了,如果做到有关边权差最小的题时,不要忘了kruskal了!