谐响应分析
任何持续的周期载荷将在结构系统中产生持续的周期响应(谐响应)。
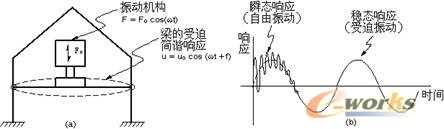
谐响应分析是用于确定线性结构在承受随时间按正弦(简谐)规律变化的载荷时的稳态响应的一种技术。
分析的目的是计算出结构在几种频率下的响应并得到一些响应值(通常是位移)对频率的曲线。从这些曲线上可以找到“峰值”响应,并进一步观察峰值频率对应的应力。
该技术只计算结构的稳态受迫振动,而不考虑发生在激励开始时的瞬态振动。谐响应分析使设计人员能预测结构的持续动力特性,从而使设计人员能够验证其设计能否成功地克服共振、疲劳,及其它受迫振动引起的有害效果。
谐响应分析是一种线性分析。任何非线性特性,如塑性和接触(间隙)单元,即使定义了也将被忽略。分析中可以包含非对称系统矩阵、流-固耦合、热结构耦合等。谐响应分析也可以分析有预应力结构,如小提琴的弦(假定简谐应力比预加的拉伸应力小得多)
谐响应求解方法
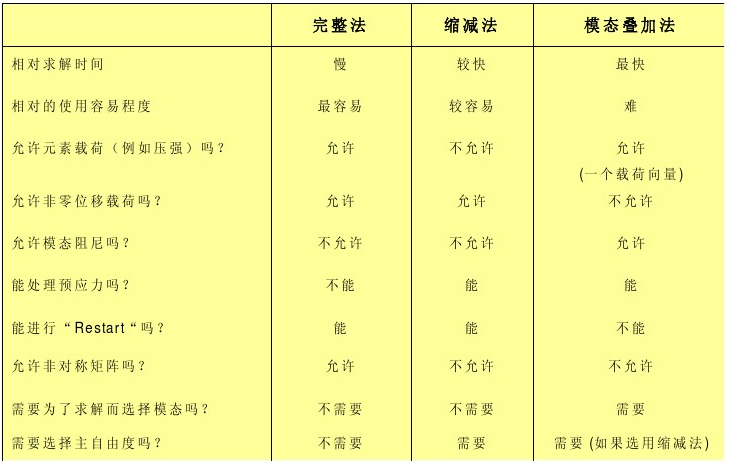
谐响应分析可采用三种方法:完全法(Full)、缩减法(Reduced)、模态叠加法(Mode Superposition)。(第四种方法,也是一种开销相对较大的方法,是将简谐载荷指定为有时间历程的载荷函数,进行相应的瞬态动力学分析,参见第三部分瞬态动力学分析中的叙述。)ANSYS/Linear Plus中只允许采用模态叠加法。
完全法
完全法是三种方法中最易使用的方法。它采用完整的系统矩阵计算谐响应(没有矩阵缩减)。矩阵可以是对称的或非对称的。
完全法的优点 是:
·容易使用,因为不必关心如何选取主自由度或振型;
·使用完整矩阵,因此不涉及质量矩阵的近似;
·允许有非对称矩阵,这种矩阵在声学或轴承问题中很典型;
·用单一处理过程计算出所有的位移和应力。
·允许定义各种类型的载荷:节点力、外加的(非零)位移、单元载荷(压力和温度)。
·允许在实体模型上定义载荷。
完全法的缺点是:
·预应力选项不可用。
·当采用Frontal方程求解器时这种方法通常比其它方法都开销大。但在采用JCG求解器或ICCG求解器时,完全法的效率很高。
缩减法
缩减法通过采用主自由度和缩减矩阵来压缩问题的规模。主自由度处的位移被计算出来后,解可以被扩展到初始的完整DOF集上(参见“模态分析”中的“矩阵缩减技术”部分关于缩减技术的细节)。
这种方法的优点是:
·在采用Frontal求解器时比完全法更快且开销小;
·可以考虑预应力效果。
缩减法的缺点是:
·初始解只计算出主自由度处的位移。要得到完整的位移、应力和力的解则需执行扩展过程(扩展过程在某些分析应用中是可选操作);
·不能施加单元载荷(压力、温度等等)
·所有载荷必须施加在用户定义的主自由度上(限制了采用实体模型上所加载荷)。
模态叠加法
模态叠加法通过对模态分析得到的振型(特征向量)乘上因子并求和来计算出结构的响应。
模态叠加法的优点是:
·对于许多问题,此法比Reduced或完全法更快且开销小;
·模态分析中施加的载荷可以通过LVSCALE命令用于谐响应分析中;
·可以使解按结构的固有频率聚集,便可得到更平滑、更精确的响应曲线图;
·可以包含预应力效果;
·允许考虑振型阻尼(阻尼系数为频率的函数)。
模态叠加法的缺点是:
·不能施加非零位移;
·在模态分析中使用PowerDynamics法时,初始条件中不能有预加的载荷
三种方法的局限性
谐响应分析的三种方法存在共同的 局限性 :
·所有载荷必须随时间按正弦规律变化;
·所有载荷必须有相同的频率;
·不允许有非线性特性;
·不计算瞬态效应。
可以通过进行瞬态动力学分析来克服这些限制,这时应将简谐载荷表示为有时间历程的载荷函数。
“瞬态动力学分析”中描述了瞬态动力学分析的过程。