红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
性质1. 节点是红色或黑色。
性质2. 根是黑色。
性质3. 所有叶子都是黑色(叶子是NIL节点)。
性质4. 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
性质5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

插入旋转
令插入的新节点为N,N的父节点为P,祖父节点为G,叔父节点为U,插入时N为红色,当P为黑色时没问题,插入旋转的原因是红红冲突,即N和P都为红色,旋转的关键在于U的颜色和N在左子树还右子树;
情形(1),U=红,令(P,U)=(黑,黑),G=红,结束,此时U在左子树or右子树无所谓;
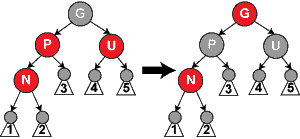
情形(2),U=黑,N在左子树,右旋转即可,P=黑,G=红;结束
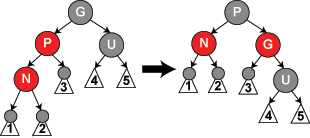
情形(3),U=黑,N在右子树,对P子树执行左旋转,变为情形(2);

插入操作最多旋转二次,是在第二种情形下;
综上所述,插入旋转的关键在叔父节点的颜色,和插入节点的左右位置;
删除旋转
如果需要删除的节点有两个儿子,那么问题可以被转化成删除另一个只有一个儿子的节点的问题,当待删除节点和孩子节点有一个为红色,易解;难点在于待删除和儿子节点都为黑色,删除后用孩子节点代替,这课子树高度减一,令被代替后的的节点为N,父节点为P,兄弟节点为S,S的左右孩子节点为SL和SR,此时已知h(N)=h-1,h(S)=h,即P的左子树高度比右子树少一,N一定为黑色,N为当前节点,由于P的左右黑高不平衡需要根据以下情况旋转:
情形(1) 当(P, S, SL,SR)= (黑,红,*,*)时,这时,由于红黑树的的固有性质,后两个*也一定为黑。对当前树进行左旋如下图,此时P子树仍不平衡,但问题转为情形(3)(4)(5),还是以N为当前节点;

情形(2) 当(P, S, SL,SR)=(黑,黑,黑,黑)时,令S=红,P子树平衡,但高度减一,以P为当前节点向上递归;
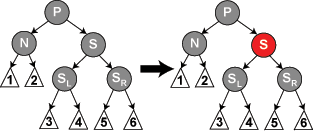
情形(3) 当(P, S, SL,SR)=(红,黑,黑,黑)时,令P=黑,S=红;平衡结束;

注:剩下的情形(黑,黑,红,黑)、(黑,黑,黑,红)/(红,黑,红,黑)、(红,黑,黑,红)归结为(*,黑,红,黑)和(*,黑,黑,红);
情形(4) 当(P, S, SL,SR)=(*,黑,红,黑)时,在S子树上执行右旋转,转为情形(5),下图未画出N和P;
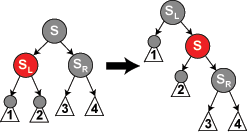
情形(5) 当(P, S, SL,SR)=(*,黑,黑,红)时,执行左旋转,完毕
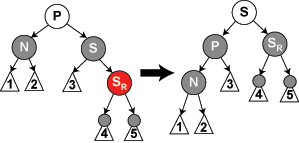
删除操作最多旋转三次,旋转序列是(1)(4)(5);
红黑树的删除旋转到此结束,删除旋转关键是看(P,S,SL,SR)的各种组合;
参考:http://zh.wikipedia.org/wiki/红黑树