实战需要掌握的内容:
1.NLopt求解器的一般使用方法
根据官网的案例:非线性约束问题
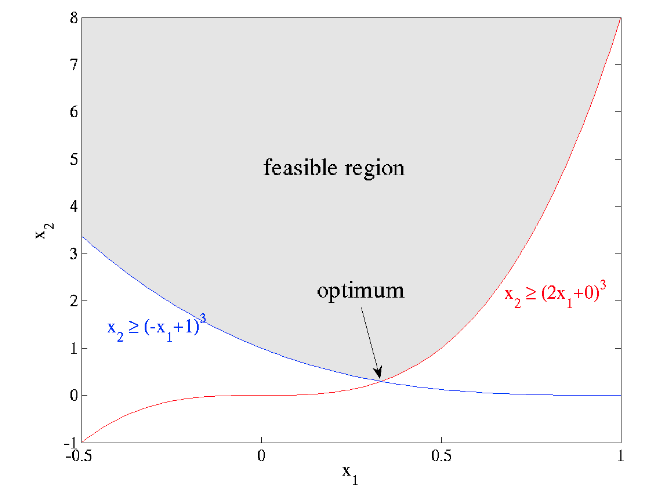
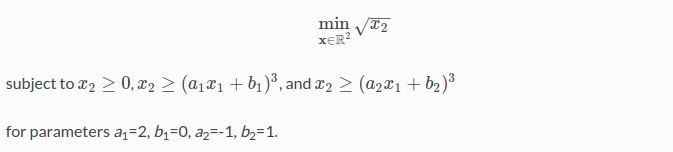
#include <iomanip> #include <iostream> #include <vector> #include <nlopt.hpp> //***************************定义objective function************************ //最优化参数的梯度,并非所有优化算法(如下)都使用梯度信息:对于列为“无衍生”的算法,grad参数将始终为空,且不需要计算 double myfunc(unsigned n, const double *x, double *grad, void *my_func_data) { if(grad) { grad[0] = 0.0; //对应x[0]的梯度,这里x是二维的。 grad[1] = 0.5 / sqrt(x[1]); //对应x[1]的梯度 } return sqrt(x[1]); //目标函数 } //************************定义一个结构体,里边是一些参数,用于表达约束******************* typedef struct { double a, b; } my_constraint_data; //***********************constraint function**************************** double myconstraint(unsigned n, const double *x, double *grad, void *data) { my_constraint_data *d = (my_constraint_data*) data; double a = d->a, b = d->b; if(grad) { grad[0] = 3 * a * (a * x[0] + b) * (a * x[0] + b); grad[1] = -1.0; } return ((a*x[0] + b) * (a*x[0] + b) * (a*x[0] + b) - x[1]); } int main() { nlopt::opt opt(nlopt::LD_MMA, 2); std::vector<double> lb(2); lb[0] = -HUGE_VAL; lb[1] = 0; opt.set_lower_bounds(lb); opt.set_min_objective(myfunc, NULL); my_constraint_data data[2] = { {2,0}, {-1,1} }; opt.add_inequality_constraint(myconstraint, &data[0], 1e-8); opt.add_inequality_constraint(myconstraint, &data[1], 1e-8); opt.set_xtol_rel(1e-4); std::vector<double> x(2); x[0] = 1.234; x[1] = 5.678; double minf; try{ nlopt::result result = opt.optimize(x, minf); std::cout << "found minimum at f(" << x[0] << "," << x[1] << ") = " << std::setprecision(10) << minf << std::endl; } catch(std::exception &e) { std::cout << "nlopt failed: " << e.what() << std::endl; } }
2.基于软约束的轨迹优化(无约束非线性优化)建模
命题如下,具体如何用代码敲出这些命题,就需要自己推导了才能理解。

下边看一下grad_traj_optimization中是怎么建模的
// --------------------------initilize NLopt---------------------------------------- nlopt::srand_time(); // int seed = ros::Time::now().toNSec() % 65536; // nlopt::srand(seed); //这里this->algorithm=24 3*num_dp是优化的维度 nlopt::opt opt(nlopt::algorithm(this->algorithm), 3 * num_dp); // x,y,z (3*n-3) x 3 optimizer = opt; //costFunc是目标函数 optimizer.set_min_objective(GradTrajOptimizer::costFunc, this); // optimizer.set_xtol_abs(1e-7); // --------------------------step specific options----------------------------- optimizer.set_maxtime(try_limit); // ---------------------------set upper and lower bound for dp-------------------- vector<double> lb, ub; lb.resize(3 * num_dp); ub.resize(3 * num_dp); //...... optimizer.set_lower_bounds(lb); optimizer.set_upper_bounds(ub); // ---------------------------set initial value--------------------------- std::vector<double> _dp(3 * num_dp); for(int i = 0; i < num_dp; ++i) { _dp[i] = Dp(0, i); _dp[i + num_dp] = Dp(1, i); _dp[i + 2 * num_dp] = Dp(2, i); } // ---------------------------optimize --------------------------- double min_f; nlopt::result result = optimizer.optimize(_dp, min_f);
NLopt形式的目标函数
/** NLopt format cost function */ double GradTrajOptimizer::costFunc(const std::vector<double> &x, std::vector<double> &grad, void *func_data) { GradTrajOptimizer *gtop = reinterpret_cast<GradTrajOptimizer *>(func_data); double cost; gtop->getCostAndGradient(x, cost, grad); return cost; }
算法24对应的是LD_MMA算法
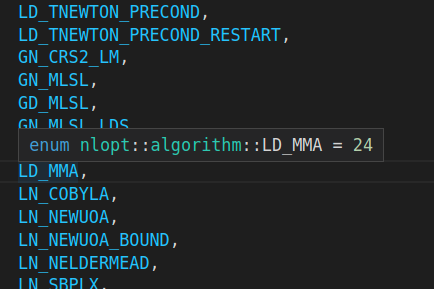
3.实践
从ROS里将其剥离,并且暂时不用SDF,得到结果如下,就算碰撞项没有,但起码应该光滑呀,不知到哪里搞错了。
