2.18比赛(T2,T3留坑)
超越一切(ak)
【题目描述】
夏洛可得到一个(h+1)×(w+1)的巧克力,这意味着她横着最多可 以切 h 刀,竖着最多可以切 w 刀 她想总共切 k 刀,每刀要么竖着切要么横着切,如果竖着切了 i 刀,横着切了 j 刀,会得到(i+1) ×(j+1)个巧克力,定义一个切 k 刀 的方案的代价是每一刀切完后巧克力个数之和,假设每刀切的位置是 随机选择的(即剩余能切的位置等概率随机选一个),请你求出期望 代价,对109+7 取模
【输入格式】
一行三个正整数 h,w,k
【输出格式】
一行一个整数表示答案
【样例 1 输入】
2 1 2
【样例 1 输出】
666666677
【数据范围】
本题有 6 个子任务,每个子任务只有 1 个测试点
对于 100%的数据,满足 h,w≤ 1018,k≤h+w
Subtask 1[10 pts]: h,w≤300
Subtask 2[10 pts]:h,w≤5000
Subtask 3[30 pts]:h,w≤106
Subtask 4[25 pts]:k≤107
Subtask 5[15 pts]:k=h+w
Subtask 6[10 pts]:无特殊限制 选手文件夹下的额外样例和最终数据范围相同
sol:题解写的非常好(大雾)


稍微解释一下,对于每一个矩形,只对它左下角的那个点记录贡献
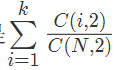 记录的是中间的点的贡献,就是不在边界上的点,这样的点共有h*w个,每个点切中的概率就是前面那个式子
记录的是中间的点的贡献,就是不在边界上的点,这样的点共有h*w个,每个点切中的概率就是前面那个式子
然后因为这是每个点的期望,统计答案时要乘以h*w
还有边上的点,对于最最左下角的点,k刀中每次切都会有1的贡献,所以ans+k
还有不在左下角的点,每次切都会新产生一个会造成贡献的点,ans+=(1+k)*k/2
标算已经在上面了,在贴一遍没什么意思,放一份较易理解的75pts的暴力好了

#include <bits/stdc++.h> using namespace std; typedef long long ll; inline ll read() { ll s=0; bool f=0; char ch=' '; while(!isdigit(ch)) { f|=(ch=='-'); ch=getchar(); } while(isdigit(ch)) { s=(s<<3)+(s<<1)+(ch^48); ch=getchar(); } return (f)?(-s):(s); } #define R(x) x=read() inline void write(ll x) { if(x<0) { putchar('-'); x=-x; } if(x<10) { putchar(x+'0'); return; } write(x/10); putchar((x%10)+'0'); return; } #define W(x) write(x),putchar(' ') #define Wl(x) write(x),putchar(' ') const ll Mod=1000000007; const ll N=20000005; ll h,w,k; ll Jiec[N],Niy[N]; inline void Ad(ll &x,ll y) { x+=y; x-=(x>=Mod)?(Mod):0; return; } inline ll Ksm(ll x,ll y) { ll ans=1ll; while(y) { if(y&1) ans=ans*x%Mod; x=x*x%Mod; y>>=1; } return ans%Mod; } inline ll C(ll n,ll m) { if(!Niy[m]) Niy[m]=Ksm(Jiec[m],Mod-2)%Mod; if(!Niy[n-m]) Niy[n-m]=Ksm(Jiec[n-m],Mod-2)%Mod; return Jiec[n]*Niy[m]%Mod*Niy[n-m]%Mod; } int main() { freopen("ak.in","r",stdin); freopen("ak.out","w",stdout); ll i; R(h); R(w); R(k); Jiec[0]=1ll; for(i=1;i<=h+w;i++) { Jiec[i]=Jiec[i-1]*i%Mod; } ll ans=0; ll NN=Ksm(C(h+w,2ll),Mod-2)%Mod; Ad(ans,C(k + 1,3ll)*NN%Mod); ans=ans*(h*w%Mod)%Mod; Ad(ans,(((1+k)*k)>>1)%Mod); Ad(ans,k); Wl(ans); return 0; } /* input 1 2 output */
附上ak王pfy的题解
