1363：小球(drop)

【题目描述】

许多的小球一个一个的从一棵满二叉树上掉下来组成FBT（Full Binary Tree，满二叉树），每一时间，一个正在下降的球第一个访问的是非叶子节点。然后继续下降时，或者走右子树，或者走左子树，直到访问到叶子节点。决定球运动方向的是每个节点的布尔值。最初，所有的节点都是false，当访问到一个节点时，如果这个节点是false，则这个球把它变成true，然后从左子树走，继续它的旅程。如果节点是true，则球也会改变它为false，而接下来从右子树走。满二叉树的标记方法如下图:

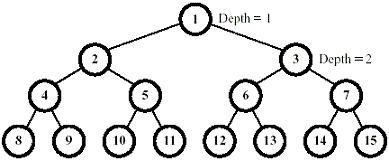
因为所有的节点最初为false，所以第一个球将会访问节点1，节点2和节点4，转变节点的布尔值后在在节点8停止。第二个球将会访问节点1、3、6,在节点12停止。明显地，第三个球在它停止之前，会访问节点1、2、5，在节点10停止。

现在你的任务是，给定FBT的深度D，和I，表示第I个小球下落，你可以假定I不超过给定的FBT的叶子数，写一个程序求小球停止时的叶子序号。

【输入】

一行包含两个用空格隔开的整数D和I。其中2≤D≤20，1≤I≤524288。

【输出】

对应输出第I个小球下落停止时的叶子序号。

【输入样例】

4 2

【输出样例】

12

#include <bits/stdc++.h>
using namespace std;

int Drop(vector<bool> &a, int i)
{
    if (i >= a.size() / 2) {
        return i;
    } else {
        a[i] = !a[i];
        if (a[i]) {
            return Drop(a, 2 * i);
        } else {
            return Drop(a, 2 * i + 1);
        }
    }
}

int main()
{
    int d = 4, i = 2;
    cin >> d >> i;
    int n = pow(2, d);
    // cout << n << endl;
    vector<bool> a(n);
    for (int k = 1; k <= i; k++) {
        int d = Drop(a, 1);
        if (k == i) {
            cout << d;
        }
    }
    return 0;
}