树
1.树的优点
有序数组: 查找很快,二分法实现的查找所需要的时间为O(logN),遍历也很快,但是在有序数组中插入,删除却需要先 找到位置,
在把数组部分元素后移,效率并不高。
链表: 链表的插入和删除都是很快速的,仅仅需要改变下引用值就行了,时间仅为O(1),但是在链表中查找数据却需要
遍历所有的元素, 这个效率有些慢了。
树的优点: 树结合了有序数组和链表的优点,可以实现快速的查找,也可以快速的删除,查找。
树的一些专用术语:
路径:
顺着连接节点的边从一个节点到另一个节点的,所经过的所有节点的顺序排列就是路径。
根:
根即是树的顶端,一个树有且只有一个根,从根到所有节点的路径有且只有一条。
父节点:
每一个节点的连接的上一个节点即是该节点的父节点。
子节点;
每一个节点的向下连接的节点即是改节点的子节点
子树:
每个节点都可以认为是一个树的根,
叶节点:
就是没有子节点的节点
层:
一个节点的层数,从根节点到该节点有多少代,就是多少层
二叉树:
树种的节点可以有多个节点,二叉树是最多只能有2个节点的树。二叉树的两个节点被称为左子节点和右子节点。
二叉树的节点是最多有2个子节点,但并不是必须有2个子节点。
平衡树和非平衡树:
如果一个树中存在一个或多个的子树,只有右子节点,或左子节点,那么这个树就是非平衡树。
2.二叉搜索树:
根节点的左右2个节点,小于根节点在放在左侧,大于根节点的放在右侧。
<1>插入
<2>查找
<3>遍历
1.中序遍历
(1)调用自身遍历节点的左子树
(2)访问这个节点
(3)调用自身遍历节点的右子树
如上图遍历过程:35,38,40,45,50,67,83
2.前序遍历
(1)访问这个节点
(2)调用自身遍历节点的左子树
(3)调用自身遍历节点的右子树
如上图遍历过程:45,38,35,40,67,50,83
3.后序遍历
(1)调用自身遍历节点的左子树
(2)调用自身遍历节点的右子树
(3)访问这个节点
如上图遍历过程:35,40,38,50,83,67,45
<4>删除
(1)删除叶节点(没有子节点的)
(2)删除节点(一个子节点的)
(3)删除节点(二个子节点的)
<5>查找最大最小值
3.二叉搜索树的代码实现
树(Tree)的代码实现:
Tree 只需要有根节点,即可访问所有的子节点,这里可以简单的定义该类,只有一个变量Root.Root类型为Node(节点对象)
该类可以实现一些操作方法大致如下:
public class Tree {
Node root;
public Tree() {
}
/**
* 删除节点
* @param key
*/
public void deldte( int key){
}
/**
* 查找节点
*
* @param key
*/
public Node find(int key){
return null;
}
/**
*
*
* @param key 插入值
* @param otherdata 插入的其他数据
*/
public void insert( int key,int otherdata){
}
/**
* 遍历二叉树
*/
public void disPlayTree(Node node){
}
节点(Node)的代码实现
Node 需要有数据项,有该类对象的左节点,右节点,还可以包含其他的数据项。实现大致如下:
public class Node {
/**
* 数据项
*/
int data;
/**
* 其他数据
*/
int otherData;
/**
* 左节点
*/
Node leftChild;
/**
* 右节点
*/
Node rightChild;
public Node() {
}
}
Tree和Node实现后,那么便可以实现里面的操作方法了。
find查找过程如图
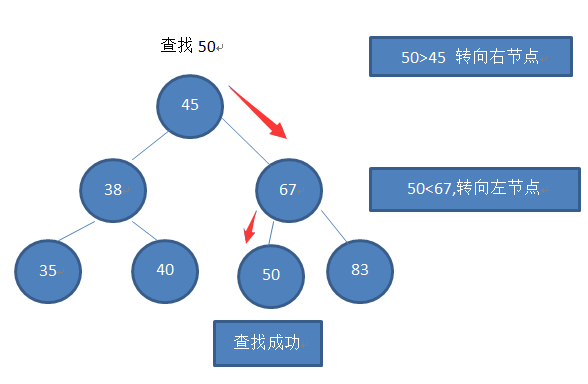
根据上图可以看出查找一个节点,最多比较次数为Tree的层数,其代码如下:
/**
* 查找节点
*
* @param key 查找的值,在该代码中为Node.data
*/
public Node find(int key){
Node current =root;
while (current.data!=key){
/**
* 小于当前节点的值,去left查找,否则去right
*/
if(key<current.data){
current=current.leftChild;
}else {
current=current.rightChild;
}
/**
* 没查找到
*/
if(current==null){
return null;
}
}
return current;
}
insert插入,插入和查找基本过程差不多,仍然是比较数据项大小,小了放在左侧,大了放其右侧。

其代码如:
/**
* @param key 插入值 node.data
* @param otherdata 插入的其他数据 node.otherdata
*/
public void insert( int key,int otherdata){
Node newNode=new Node();
newNode.data=key;
newNode.otherData=otherdata;
if(root==null){
root=newNode;
}else{
Node current=root;
Node parent;
while (true)
{
parent=current;
if(key<current.data){
current=current.leftChild;
if(current==null){
parent.leftChild=newNode;
return;
}
}else{
current=current.rightChild;
if(current==null){
parent.rightChild=newNode;
return;
}
}
}
}
}
遍历二叉搜索树
二叉树的中序遍历过程是调用自身左子树,然后访问节点,在调用自身右子树。递归代码如下。而前序和后序的遍历只需要把中序遍历
中的调用自身的递归和访问节点(就是打印那一行)翻翻顺序就ok了。
/**
* 递归遍历二叉树(中序)
*/
public void disPlayTree(Node node){
if(node!=null){
if(node.leftChild!=null){
disPlayTree(node.leftChild);
}
Log.d("", "二叉树遍历: "+node.data);
if(node.rightChild!=null){
disPlayTree(node.rightChild);
}
}
}
删除:delete节点。如果待删除节点是叶节点(没有子节点),值直接把删除节点赋值为null即可。
如果有一个子节点也简单,待删除的节点在删除节点的左侧(右侧),则把待删除节点的子树赋值给待删除节点父节点的
左侧(右侧)。
删除:如果删除节点右2个子节点,则需要先找到待删除节点的后续节点,即是比待删除节点次高的节点。
如图:

删除过程就是:87位后续节点,为50的右节点。62为87的左节点。89位87的右节点。

删除:后续节点在左侧时:

查找到后续节点是77,则50的右节点为77,79变成87的左节点,93还是83的右节点。62变成77的左节点。

删除代码实现:
1.获取后续节点
/**
* 获取后序节点
*/
public Node getSuccessor(Node delNode){
Node successorParent =delNode;
Node successor=delNode;
Node current=delNode.rightChild;
while(current!=null){
successorParent=successor;
successor=current;
current=current.leftChild;
}
if(successor!=delNode.rightChild){
successorParent.leftChild=successor.rightChild;
successor.rightChild=delNode.rightChild;
}
Log.d("二叉树遍历", "getSuccessor: "+successor.data);
return successor;
}
删除节点:
/**
* 删除节点
* @param key
*/
public boolean deldte( int key){
Node current=root;
Node parent=root;
boolean isLeftChild=true;
/**
* 先把删除值的Node找出来
*/
while(current.data!=key){
parent=current;
if(key<current.data){
isLeftChild=true;
current=current.leftChild;
}else {
isLeftChild=false;
current=current.rightChild;
}
if(current==null){
return false;
}
} // while结束,查找到删除节点,就是current
/**
* 如果删除节点是叶节点
*/
if(current.leftChild==null&¤t.rightChild==null){
if(current==root){
root=null;
}else if(isLeftChild){
parent.leftChild=null;
}else{
parent.rightChild=null;
}
}
/**
* 如果删除的节点没有rightChild,只有leftChild
*/
else if(current.rightChild==null){
if(current==root){
root=current.leftChild;
}
else if(isLeftChild){
parent.leftChild=current.leftChild;
}
else {
parent.rightChild=current.leftChild;
}
}
/**
* 如果删除的节点只有rightChild
*/
else if(current.leftChild==null){
if(current==root){
root=current.rightChild;
}
else if(isLeftChild){
parent.leftChild=current.rightChild;
}else{
parent.rightChild=current.rightChild;
}
}
/**
* 如果删除点有2个节点
*/
else {
/**
* 获取后续节点
*/
Node successor=getSuccessor(current);
if(current==root){
root=successor;
}else if( isLeftChild){
parent.leftChild=successor;
}else{
parent.rightChild=successor;
}
successor.leftChild=current.leftChild;
}
return true;
}
找最大最小值:

寻找最大最小值 这个就简单了,从根节点一直找左节点直到没有左子节点,那么这个值就是最小值,反之就是最大值。
4.小结:
代码:
http://pan.baidu.com/s/1miz8ocC

https://github.com/galibujianbusana/MyErChaShu

