1. KingdomAndTrees
给出n个数a[1..n],求一个数组b[1..n]满足b严格递增,且b[1]>=1。
定义代价为W = max{abs(a[i]-b[i])},求代价最小值。
n<=50
【题解】
二分代价W,贪心判断。当前肯定越小越优,如果下一个加上当前二分的值,小于等于当前这个,那么就肯定不行,依次判即可。

// BEGIN CUT HERE // END CUT HERE #line 5 "KingdomAndTrees.cpp" # include <vector> # include <stdio.h> # include <string.h> # include <iostream> # include <algorithm> using namespace std; typedef long long ll; typedef long double ld; typedef unsigned long long ull; const int M = 50 + 10; const int INF = 1e9; class KingdomAndTrees { public: int n, h[M]; inline bool chk(int x) { int lst = max(h[1]-x, 1); for (int i=2; i<=n; ++i) { if(h[i]+x <= lst) return false; lst = max(h[i]-x, lst+1); } return true; } int minLevel(vector<int> heights) { int l = 0, r = 2e9, mid, ans; n = heights.size(); for (int i=0; i<n; ++i) h[i+1] = heights[i]; while(1) { if(r-l <= 3) { for (int i=l; i<=r; ++i) if(chk(i)) { ans = i; break; } break; } mid = l+r>>1; if(chk(mid)) r = mid; else l = mid; } return ans; } };
2. KingdomAndDice
给出n个数a[1..n],再给出n个数b[1..n],a中有些数为0,你要把其中一些0改成不大于X的数,满足:任意不大于X的正整数最多在a和b中共出现1次。
令p为随机选1<=i,j<=n,使得ai>bj的概率,求使|p-0.5|最小的p值。
n<=50
【题解】
看成贡献,每个ai>bj相当于贡献+1。就使得贡献和n*n/2最接近即可。
b数组把[0,X]分成了n+1段,a如果在第i段内的贡献为i-1,容易看出在第1段中一定可以不改(本来就是0),所以第1段忽略,其他往上整(现在就是在第i段内贡献为i)
考虑dp:f[i,j,k]表示在前i段中,有了j个0,贡献为k,是否可行。
那么枚举当前段选了几个。这个的上限可以通过预处理求得。
然后直接转移即可。时间复杂度O(n^5)

// BEGIN CUT HERE // END CUT HERE #line 5 "KingdomAndDice.cpp" # include <math.h> # include <vector> # include <stdio.h> # include <string.h> # include <iostream> # include <algorithm> using namespace std; typedef long long ll; typedef long double ld; typedef unsigned long long ull; const int M = 50 + 10; const int INF = 1e9; class KingdomAndDice { public: bool f[M][M][M*M]; int n, a[M], b[M], len[M], m; double newFairness(vector <int> firstDie, vector <int> secondDie, int X) { memset(f, 0, sizeof f); int pre = 0; n = firstDie.size(); m = 0; for (int i=1; i<=n; ++i) { a[i] = firstDie[i-1]; b[i] = secondDie[i-1]; m += (a[i] == 0); } sort(a+1, a+n+1); sort(b+1, b+n+1); // for (int i=1; i<=n; ++i) cout << a[i] << ' '; cout << endl; // for (int i=1; i<=n; ++i) cout << b[i] << ' '; cout << endl; for (int i=1; i<n; ++i) len[i] = b[i+1] - b[i] - 1; len[n] = X - b[n]; for (int i=1; i<=n; ++i) { if(a[i] == 0) continue; int tem = 0; for (int j=1; j<=n; ++j) if(a[i] > b[j]) ++tem; if(tem) len[tem] --; pre += tem; } // for (int i=1; i<=n; ++i) cout << len[i] << ' '; // cout << endl; for (int j=0; j<=m; ++j) f[0][j][pre] = 1; for (int i=1; i<=n; ++i) for (int j=0; j<=m; ++j) for (int k=0; k<=n*n; ++k) for (int cur=0, to = min(j, len[i]); cur<=to; ++cur) if(k-i*cur >= 0) { // if(f[i-1][j-cur][k-i*cur] == 1 && f[i][j][k] == 0) // printf("f[%d,%d,%d] --> f[%d,%d,%d] ", i-1, j-cur, k-i*cur, i, j, k); f[i][j][k] |= f[i-1][j-cur][k-i*cur]; } double ans = 1e9, E = (double)n*n, id; for (int i=0; i<=n*n; ++i) { if(f[n][m][i]) { // cout << i << endl; if(fabs(2*i-E) < ans) { ans = fabs(2*i-E); id = i; } } } return id/n/n; } };
这其实是一个多重背包,把枚举的那个部分用二进制拆分,然后用01背包做就能做到O(n^4logn)的复杂度。
发现是bool数组的转移,把转移用bitset维护,就能做到O(n^4logn/32)的复杂度。
其实状态也是可以优化的(可以不记录j这维,把bool数组改成int,存j),这样就能做到O(n^3logn)的复杂度,好像和bitset的复杂度差不多?
不管了反正n=50我就写O(n^5)
其他。。待填坑。
3.KingdomAndCities
求n个点m条边,前K个点度数均为2的无向连通图的个数,无重边自环。
n,m<=50,K<=2
【题解】
考虑k=0的情况,就是求n个点m条边的无向连通图个数。
令f(i,j)表示i个点j条边的无向连通图个数。令E(i)表示i个点的无向完全图的边数。
考虑补集转换,全部方案为C(E(i),j)。
枚举第一个点包含的连通块的大小k以及里面的边l。
那么一种(k,l)对应的方案数有C(i-1,k-1)*C(E(i-k),j-l)*f[k][l]
从i-1个点(除了1)选出k-1个点跟1号点在一个连通块。另外一个部分连通不连通都行,方案就是C(E(i-k),j-l),然后乘上1号点包含的连通块个数。
总的方程式就是

那么我们会K=0的情况了。
下面的图红色表示即将被删除,蓝色表示即将被加入,黑色表示本来就有。
在讨论1<=K<=2的情况前,我们不妨思考这样一个结论:
在每种方案中,限定度数为2的点要么用来取代一个边,延长一个链,要么用来加到一个边的两个端点上,构成一个环。
特殊的,当K=2时候可能存在加到一个点上,构成三元环。
比如:
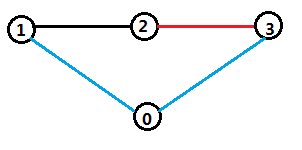
这种就不符合上面三种情况,所以这种情况可以看作1、3之间原来有边,用0来延长这条边。
类似的,所有其他不符合上面三种情况,都已经被上面两种情况包含的方案计算过了。
1. 对于K=1:
①延长链
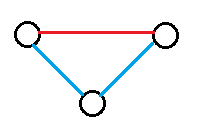
从f[n-1,m-1]转移来,有m-1个边可以作为延长对象。
②构成环
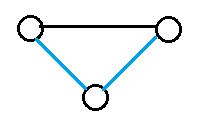
从f[n-1,m-2]转移来,有m-1个边可以作为构成环的对象。
综上,我们完成了对K=1的分类讨论。实现见代码。
2. 对于K=2:
①两个连一起,延长链
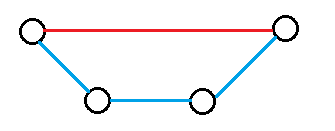
从f[n-2,m-2]转移来,有m-2条边可以作为延长的对象,延长后0/1的摆放位置有2种(0前1后,0后1前)
②两个连一起,构成环
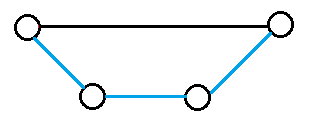
从f[n-2,m-3]转移来,有m-3条边可以作为构成环的对象,0/1的摆放位置同样有2种。
③延长两条边
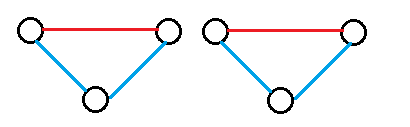
从f[n-2,m-2]转移来,有(m-2)*(m-3)/2对组合可以加,0/1的摆放位置有2种。
④两个点分别构成环
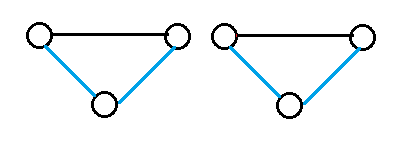
从f[n-2,m-4]转移来,有(m-4)*(m-5)/2对组合可以加,0/1的摆放位置有2种。
⑤一个点构成环,一个点延长链
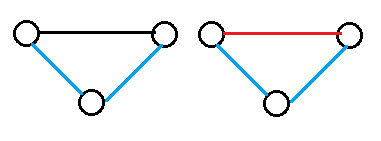
从f[n-2,m-3]转移来,有(m-3)*(m-4)/2对组合可以加,0/1的摆放位置有2种,构成环/延长链也有2种。
⑥在同一条边上构成2个环
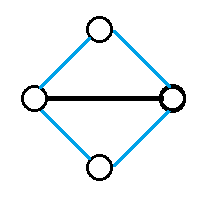
从f[n-2,m-4]转移来,有m-4条边可以作为构成2个环的对象。由于对称不存在顺序。
⑦在同一条边上分别延长
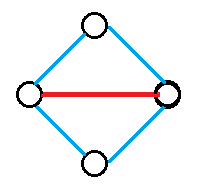
从f[n-2,m-3]转移来,有m-3条边可以作为延长对象。由于对称不存在顺序。
⑧在一个点上构成一个环。
假设红色的那个点是本来存在的。
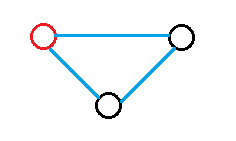
从f[n-2,m-3]转移来,有n-2个点可以作为成环对象。由于对称不存在顺序
我们终于讨论完K=2了!
然后就很简单了。。

// BEGIN CUT HERE // END CUT HERE #line 5 "KingdomAndCities.cpp" # include <vector> # include <stdio.h> # include <string.h> # include <iostream> # include <algorithm> using namespace std; typedef long long ll; typedef long double ld; typedef unsigned long long ull; const int M = 50 + 10, N = 2500 + 10; const int INF = 1e9, mod = 1e9 + 7; class KingdomAndCities { public: int f[M][M]; int C[N][N]; inline int E(int n) { return n * (n-1) / 2; } int howMany(int n, int K, int m) { if(n == 1) return (m==0 && K==0); if(n == 2) return (m==1 && K==0); C[0][0] = 1; for (int i=1; i<=2500; ++i) { C[i][0] = 1; for (int j=1; j<=i; ++j) { C[i][j] = C[i-1][j] + C[i-1][j-1]; if(C[i][j] >= mod) C[i][j] -= mod; } } for (int i=1; i<=n; ++i) for (int j=0; j<=m; ++j) { f[i][j] = C[E(i)][j]; for (int k=1; k<=i-1; ++k) { int res = 0; for (int l=k-1, lto = min(E(k), j); l<=lto; ++l) { res = res + 1ll * C[E(i-k)][j-l] * f[k][l] % mod; if(res >= mod) res -= mod; } res = 1ll * res * C[i-1][k-1] % mod; f[i][j] -= res; if(f[i][j] < 0) f[i][j] += mod; } } // f(n,m) 表示n个点m条边的无向连通图的个数 if(K == 0) return f[n][m]; ll ans = 0; if(K == 1) { // K = 1 if(m >= 1) (ans += 1ll * f[n-1][m-1] * (m-1) % mod) %= mod; if(m >= 2) (ans += 1ll * f[n-1][m-2] * (m-2) % mod) %= mod; } else { // K = 2 if(m >= 2) (ans += 1ll * f[n-2][m-2] * 2 * (m-2) % mod) %= mod; if(m >= 3) (ans += 1ll * f[n-2][m-3] * 2 * (m-3) % mod) %= mod; if(m >= 2) (ans += 1ll * f[n-2][m-2] * (m-2) * (m-3) % mod) %= mod; if(m >= 3) (ans += 1ll * f[n-2][m-3] * 2 * (m-3) * (m-4) % mod) %= mod; if(m >= 4) (ans += 1ll * f[n-2][m-4] * (m-4) * (m-5) % mod) %= mod; if(m >= 3) (ans += 1ll * f[n-2][m-3] * (m-3) % mod) %= mod; if(m >= 4) (ans += 1ll * f[n-2][m-4] * (m-4) % mod) %= mod; if(m >= 3) (ans += 1ll * f[n-2][m-3] * (n-2) % mod) %= mod; if(m >= 2) (ans += 1ll * f[n-2][m-2] * (m-2) * (m-3) % mod) %= mod; } return ans; } };
