传送门:http://www.lydsy.com/JudgeOnline/problem.php?id=3328
【题解】
真心巧妙。
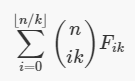
这个式子看起来不大好,稍作化简。
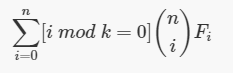
斐波那契数列第n项是斐波那契矩阵的n次方的左上角的数。
化成矩阵形式。
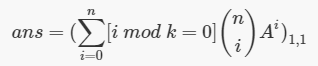
考虑二项式定理的矩阵形式。

就差一个[i mod k = 0]不对了,我们就需要构造一个式子,使得当i mod k = 0的时候该式子为1,否则为0.
考虑单位根,原根。
令g为原根,那么单位根w=g^((n-1)/k),且题目保证了k|n-1。
那么对于i属于[0,k-1],当且仅当i=0的时候,w^i=1。
那么构造

这个式子当i mod k=0的时候,w^i=k,否则为0.
进一步,除以一个k就能完成要求了。
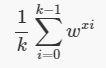
然后我们将这个代入ans。
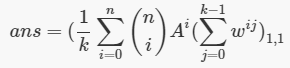
我们设B为答案矩阵,B[1,1]即为ans,那么

稍加转换

提前sigma,交换位置
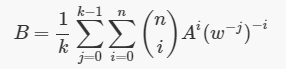
那么我们构造
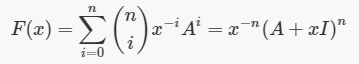
观察形式,那么答案就是
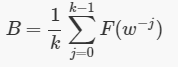
我们枚举k,然后快速幂计算F即可。

# include <stdio.h> # include <string.h> # include <iostream> # include <algorithm> // # include <bits/stdc++.h> using namespace std; typedef long long ll; typedef long double ld; typedef unsigned long long ull; const int M = 5e5 + 10; # define RG register # define ST static ll n; int k, mod; int g, w, inv, ans; struct mat { int a, b, c, d; friend mat operator * (mat a, mat b) { mat c; c.a = (1ll * a.a * b.a + 1ll * a.b * b.c) % mod; c.b = (1ll * a.a * b.b + 1ll * a.b * b.d) % mod; c.c = (1ll * a.c * b.a + 1ll * a.d * b.c) % mod; c.d = (1ll * a.c * b.b + 1ll * a.d * b.d) % mod; return c; } friend mat operator ^(mat a, ll b) { mat ret = a; --b; while(b) { if(b&1) ret = ret * a; a = a * a; b >>= 1; } return ret; } }A; inline int pwr(int a, ll b) { int ret = 1; while(b) { if(b&1) ret = 1ll * ret * a % mod; a = 1ll * a * a % mod; b >>= 1; } return ret; } int y[M], yn; inline int G() { yn = 0; int t = mod-1; for (int i=2; i*i<=t; ++i) { if(t%i == 0) { y[++yn] = i; if(i*i != t) y[++yn] = t/i; } } bool gg = 0; int g = 2; while(1) { gg = 0; for (int i=1; i<=yn; ++i) if(pwr(g, y[i]) == 1) { gg = 1; break; } if(!gg) return g; ++g; } } inline int F(int x) { A.a = x+1, A.b = A.c = 1, A.d = x; A = A ^ n; x = pwr(x, mod-2); x = pwr(x, n); return 1ll * x * A.a % mod; } void sol() { cin >> n >> k >> mod; g = G(); w = pwr(g, (mod-1)/k); inv = pwr(w, mod-2); ans = 0; // cout << w << endl; for (int i=0, x=1; i<k; ++i, x = 1ll * x * inv % mod) { ans = ans + F(x); if(ans >= mod) ans -= mod; } ans = 1ll * ans * pwr(k, mod-2) % mod; ans = (ans + mod) % mod; cout << ans << endl; } int main() { int T; cin >> T; while(T--) sol(); return 0; }
