java数据结构----图

1.图：.在计算机程序设计中，图是最常用的数据结构之一。对于存储一般的数据问题，一般用不到图。但对于某些（特别是一些有趣的问题），图是必不可少的。图是一种与树有些相像的数据结构，从数学意义上来讲，树是图的一种。而在计算机程序设计中，图的应用方式与树不同。图通常有一个固定的形状，这是由物理或抽象的问题所决定的。例如图中节点表示城市，而边可能表示城市间的班机航线。当讨论图时，节点通常叫做顶点，

2.一些概念：

　　图：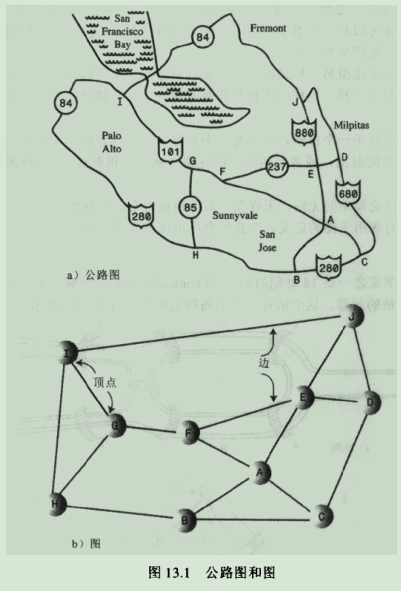

　　说明：为引入概念，我们用图13.1a来表示美国某处的简化高速公路网，图13.1b来表示模拟这些告诉公路的图。在图中，圆圈代表高速公路的交汇点，连接圆圈的直线代表告诉公路段，圆圈是顶点，线是边。顶点通常用一些方法来标识----正如图中表示的那样，用字母表中的字母来表示。每条边由两个顶点作为两边。图并不是要试图反映地图上的地理位置。它只是反映了顶点和边的关系----即那些边连接着哪些顶点。它本身不涉及物理的远近和方向。而且一条边可能表示几条可能的公路。两个交叉点之间的连通性（或不连通性）是重要的，而实际的路线并不重要。

　　a.邻接：如果两个顶点被同一条边连接，就称这两个顶点是邻接的。图13.1中，顶点I 和G是邻接的，但I 和 F 就不是。和某个指定顶点邻接的顶点有时叫它的邻居。如G 的邻居是I，H和F.

　　b.路径：路径是边的序列，图13.1显示了一条从顶点B到顶点J的路径，这条路径通过了A,E,这条路径称作BAEJ。这两个顶点之间还有其他路径，如BCDJ.

　　

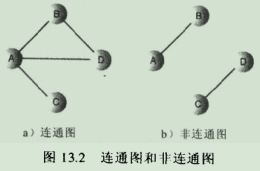
　　c.连通图：如果至少有一条路径，可以连接起所有的顶点，那么这个图被称作连通的，如图13.2a。如果不能从这里到那里，那么这个图就是非连通的。如13.2b。非连通图包含几个连通子图。在图13.2b中，A和B是一个连通子图，C和D也是一个连通子图。

　　d.有向图和带权图：图13.1和图13.2中的图是无向图，这说明图中的边没有方向----可以从任意一边到另为一边。所以可以从顶点A到顶点B,或者从顶点B到顶点A。两者是等价的（无向图很好的反映了高速公路网，因为在一条公路上可以按两个方向行驶），然而图还经常被用来模拟另一种情况，即只能沿着边向一个方向行驶。这样的图被称作是有向的。允许移动的方向通常是用一端带有箭头的方向表示。在某些图中，边被赋予一个权值，权值是一个数字，他能代表两个顶点间的物理距离，或从一个顶点到另一个顶点的时间，或者是两点间的花费（如飞机航班），这样的图称为带权图。

3.程序中如何表示图：

　　3.1.顶点：在非常抽象的图的问题中，知识简单的把顶点编号，从0->n-1,不需要任何变量类型来存储顶点，因为他们的用处来自于他们之间的相互关系，但大多数情况下，顶点表示某个真实世界的对象。顶点对象能放在数组中，然后用下标指示。

　　3.2.边：图并不像树，拥有几种固定的结构，二叉树中顶点最多有两个子节点，但图的每个顶点可以与任意多个顶点相连。为此，一般用两个方法表示图，邻接矩阵和邻接表。（如果一条边连接两个顶点，那么这两个顶点就是邻接的）

　　　　3.2.1.邻接矩阵：它是一个二维数组，数据项表示两点间是否存在边，如果图有N个顶点，邻接矩阵就是N * N 的数组。表13.1显示了图13.1a中图的邻接矩阵。

　　　　图：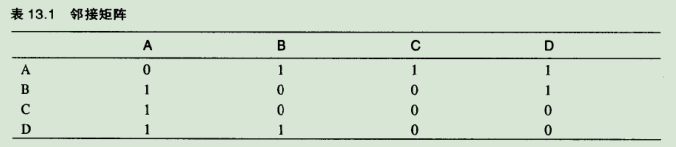

　　　　说明：顶点被用作行和列的标题，这两个顶点间右边则标识为1，无边则标识为0.（也可用boolean值表示），如图所示，顶点A 和另为3个顶点邻接，B和A,D邻接，C只与A邻接。而D与A和B邻接。从A-A到D-D称为主对角线，顶点和自身的连接设为0。也可设为1.

　　　　3.2.2.邻接表：表指的是链表，实际上，邻接表是一个链表数组。每个单独的链表表示了有哪些顶点和当前顶点邻接。表13.2显示了13.2a中图的邻接表。

　　　　图：

　　　　说明：本表中符号-->表示链表中的一个节点，链表中每个节点都是一个顶点，链表中的每个节点都是一个顶点，在这里的每个链表中，顶点按字母顺序排列，不过这并不是必须的。不要把邻接表的内容与路径混淆，邻接表表示了当前节点与那些节点相连------即，两个节点间存在边，而不是表示顶点间的路径。

4.图的搜素：图中实现的最基本的操作之一就是搜索从一个指定顶点可以到达那些顶点。有两种常用的方法来搜索树，深度优先搜索（DFS）和广度优先搜索（BFS）,他们最终都会到达所有连通的顶点，深度优先搜索通过栈来实现，而广度优先搜索通过队列来实现。

　　4.1.深度优先搜索：找到一个起始点---本例为顶点A,需要做三件事情，首先访问该节点，然后把该点放入栈中，以便记住它，最后标记该点，这样就不会再访问它了。

　　　　4.1.1.图解：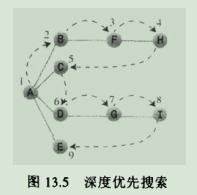

　　　　4.1.2.主要规则：

　　　　　　4.1.2.1.规则1：如果可能，访问一个邻接的未访问顶点，标记它，并把他放入栈中。

　　　　　　4.1.2.2.规则2：当不能执行规则1时，如果栈非空，就从栈中弹出一个顶点。

　　　　　　4.1.2.3.规则3：如果不能执行规则1和规则2，就完成了整个搜索过程。

　　4.2.广度优先搜索：首先访问起始顶点的所有邻接点，然后再访问较远的区域，用队列来实现它。（A是起始点，所以访问它，并标记为当前顶点，然后应用规则）

　　　　4.2.1图解：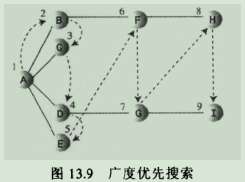

　　　　4.2.2.主要规则：

　　　　　　4.2.2.1.规则1：访问下一个问来访问的邻接点（如果存在），这个顶点必须是当前顶点的邻接点，标记它，并把它插入到队列中。

　　　　　　4.2.2.2.规则2：如果因为已经没有未访问顶点而不能执行规则1，那么从队列头取一个顶点（如果存在），并使其成为当前顶点。

　　　　　　4.2.2.3.规则3：如果因为队列为空而不能执行规则2，则搜索结束。

5.深度优先搜索实现：

　　5.1.StackX.java

package com.cn.graph;
/**
 * 图的深度优先搜索底层---栈类
 * @author Administrator
 *
 */
public class StackX {
private final int SIZE = 20;
private int[] st;
private int top;
public StackX(){
    st = new int[SIZE];
    top = -1;
}
public void push(int j){
    st[++ top] = j;
}
public int pop(){
    return st[top --];
}
public int peek(){
    return st[top];
}
public boolean isEmpty(){
    return top == -1;
}
}

　　5.2.Vertex.java

package com.cn.graph;
/**
 * 图的顶点类
 * @author Administrator
 *
 */
public class Vertex {
public char lable;
public boolean wasvisited;
public Vertex(char lab){
    lable = lab;
    wasvisited = false;
}
}

　　5.3.Graph.java

package com.cn.graph;
/**
 * 深度优先实现的图
 * @author Administrator
 *
 */
public class Graph {
private final int MAX_VERTS = 20;
private Vertex[] vertexList;
private int adjMat[][];
public int nVerts;
private StackX theStack;
public Graph(){
    vertexList = new Vertex[MAX_VERTS];
    adjMat = new int[MAX_VERTS][MAX_VERTS];
    nVerts = 0;
    for (int i = 0; i < MAX_VERTS; i++) {
        for (int j = 0; j < MAX_VERTS; j++) {
            adjMat[i][j] = 0;
        }
    }
    theStack = new StackX();
}
public void addVertex(char lab){
    vertexList[nVerts ++] = new Vertex(lab);
}
public void addEdage(int start,int end){
    adjMat[start][end] = 1;
    adjMat[end][start] = 1;
}
public void displayVertex(int v){
    System.out.print(vertexList[v].lable+" ");
}
public void dfs(){
    vertexList[0].wasvisited = true;
    displayVertex(0);
    theStack.push(0);
    while (! theStack.isEmpty()){
        int v = getAdjUnvisitedVertex(theStack.peek());
        if (v == -1)
            theStack.pop();
        else{
            vertexList[v].wasvisited = true;
            displayVertex(v);
            theStack.push(v);
        }
    }
    for (int i = 0; i < nVerts; i++) 
        vertexList[i].wasvisited = false;
}
public int getAdjUnvisitedVertex(int v){
    for (int i = 0; i < nVerts; i++)
        if (adjMat[v][i] == 1 && vertexList[i].wasvisited == false)
            return i;
    return -1;
}
}

　　5.4.GTest.java

package com.cn.graph;
/**
 * 深度优先搜索测试类
 * @author Administrator
 *
 */
public class GTest {
public static void main(String[] args) {
    Graph g = new Graph();
    g.addVertex('A');
    g.addVertex('B');
    g.addVertex('C');
    g.addVertex('D');
    g.addEdage(0, 1);
    g.addEdage(2, 1);
    g.addEdage(2, 3);
//    g.displayVertex(0);
    g.dfs();
}
}

6.广度优先搜索实现：

　　6.1.Queue.java

package com.cn.graph;
/**
 * 图的广度优先搜索---队列类
 * @author Administrator
 *
 */
public class Queue {
private final int SIZE = 20;
private int queueArray[];
private int front;
private int rear;
public Queue(){
    queueArray = new int[SIZE];
    front = 0;
    rear = -1;
}
public void insert(int j){
    if (rear == SIZE - 1)
        rear  = -1;
    queueArray[++ rear] = j;
}
public int remove(){
    int temp = queueArray[front ++];
    if (front == SIZE)
        front = 0;
    return temp;
}
public boolean isEmpty(){
    return (rear + 1 == front || front + SIZE - 1 == rear);
}
}

　　6.2.Vertex.java

package com.cn.graph;
/**
 * 图的顶点类
 * @author Administrator
 *
 */
public class Vertex {
public char lable;
public boolean wasvisited;
public Vertex(char lab){
    lable = lab;
    wasvisited = false;
}
}

　　6.3.QGraph.java

package com.cn.graph;
/**
 * 广度优先搜索----队列实现
 * @author Administrator
 *
 */
public class QGraph {
    final int MAX_VERTS = 20;
    private Vertex[] vertexList;
    private int adjMat[][];
    public int nVerts;
    private Queue thequeue;
    public QGraph(){
        vertexList = new Vertex[MAX_VERTS];
        adjMat = new int[MAX_VERTS][MAX_VERTS];
        nVerts = 0;
        for (int i = 0; i < MAX_VERTS; i++) 
            for (int j = 0; j < MAX_VERTS; j++) 
                adjMat[i][j] = 0;
        thequeue = new Queue();
    }
    public void addVertex(char lab){
        vertexList[nVerts ++] = new Vertex(lab);
    }
    public void addEdage(int start,int end){
        adjMat[start][end] = 1;
        adjMat[end][start] = 1;
    }
    public void displayVertex(int v){
        System.out.print(vertexList[v].lable+" ");
    }
    public void bfs(){
        vertexList[0].wasvisited = true;
        displayVertex(0);
        thequeue.insert(0);
        int v2;
        while (! thequeue.isEmpty()){
            int v = thequeue.remove();
            while ((v2 = getAdjUnvisitedVertex(v)) != -1){
                vertexList[v2].wasvisited = true;
                displayVertex(v2);
                thequeue.insert(v2);
            }
            }
        for (int i = 0; i < nVerts; i++) 
            vertexList[i].wasvisited = false;
    }
    public int getAdjUnvisitedVertex(int v){
        for (int i = 0; i < nVerts; i++)
            if (adjMat[v][i] == 1 && vertexList[i].wasvisited == false)
                return i;
        return -1;
    }

}

　　6.4.QGTest.java

package com.cn.graph;
/**
 * 广度优先搜索实现
 * @author Administrator
 *
 */
public class QGTest {
public static void main(String[] args) {
    QGraph q = new QGraph();
    q.addVertex('a');
    q.addVertex('b');
    q.addVertex('c');
    q.addVertex('d');
    q.addEdage(0, 1);
    q.addEdage(2, 1);
    q.addEdage(0, 3);
    q.bfs();
    
}

}

7.最小生成树（MST）：最小生成树边E的数量总比顶点V 的数量小1。E = V - 1;

8.深度优先实现MST的核心代码：

　　Graph + .

public void mst(){
    vertexList[0].wasvisited = true;
    theStack.push(0);
    while (! theStack.isEmpty()){
        int currentVertex = theStack.peek();
        int v = getAdjUnvisitedVertex(currentVertex);
        if (v == -1)
            theStack.pop();
        else{
            vertexList[v].wasvisited = true;
            theStack.push(v);
            displayVertex(currentVertex);
            displayVertex(v);
            System.out.print(" ");
        }
    }
    for (int i = 0; i < nVerts; i++) {
        vertexList[i].wasvisited = false;
    }
}

9.有向图的应用场景案例：

　　9.1.场景图示：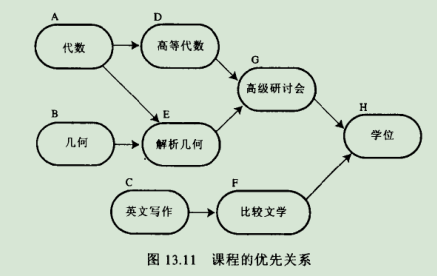

　　　　9.1.1.有向图：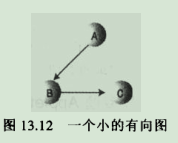

　　　　9.1.2.图13.12对应的邻接矩阵：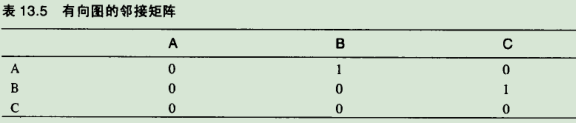

　　　　9.1.3.拓扑排序：假设存在一个课程列表，包含了要得到学位必修的所有课程，就像图13.11所示的课程一样，下面按照课程的先后关系排列它们。得到学位是列表的最后一项，这就得到BAEDGCFH的序列。这种方式的排列叫做为图进行拓扑排序。同样，CFBAEDGH也满足优先关系。当使用算法生成一个拓扑序列时，使用的方法和代码细节决定了生成那种拓扑序列。

　　　　9.1.4.拓扑排序算法的核心步骤：a.找到一个没有后继的节点。b.从图中删除这个顶点，在列表的前面插入顶点的标记。重复步骤a,b 直到所有顶点都从图中删除。这时列表显示的顶点顺序就是拓扑排序结果。拓扑排序可以用于连通图也可以用于非连通图。

10.wallshall算法：需要很快找到是否一个顶点可以从其他顶点到达。可以构建一个表，这个表以O(1)的时间复杂度告知一个顶点到另一个顶点是否可达，这样的表可以通过修改图的邻接矩阵实现。wallshall算法的核心思想：如果能从顶点L到达M,并且能从顶点M到达N，那么可以从L 到 N.