hdu-2604 Queuing---递推+矩阵快速幂

题目链接：

https://vjudge.net/problem/HDU-2604

题目大意：

n个人排队，f表示女，m表示男，包含子串‘fmf’和‘fff’的序列为O队列，否则为E队列，有多少个序列为E队列。

解题思路：

用f(n)表示n个人满足条件的结果，那么如果最后一个人是m的话，那么前n-1个满足条件即可，就是f(n-1)； 
如果最后一个是f那么这个还无法推出结果，那么往前再考虑一位：那么后三位可能是：mmf, fmf, mff, fff，其中fff和fmf不满足题意所以我们不考虑，但是如果是 
mmf的话那么前n-3可以找满足条件的即：f(n-3)；如果是mff的话，再往前考虑一位的话只有mmff满足条件即：f(n-4) 
所以f(n)=f(n-1)+f(n-3)+f(n-4)，递推会超时，可用矩阵快速幂 
构造一个矩阵：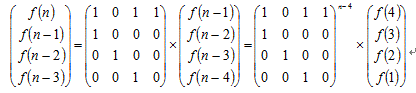 

#include<bits/stdc++.h>
using namespace std;
int MOD;
struct Mat
{
    int a[4][4];
    int n, m;//n为行数，m为列数
    Mat(int n, int m):n(n), m(m)
    {
        memset(a, 0, sizeof(a));
    }
    void init()
    {
        for(int i = 0; i < n; i++)a[i][i] = 1;//初始化成单位矩阵
    }
    void output()
    {
        for(int i = 0; i < n; i++)
        {
            for(int j = 0; j < m; j++)
            {
                cout<<a[i][j]<<" ";
            }
            cout<<endl;
        }
    }
};
Mat mul(Mat a, Mat b)//矩阵乘法
{
    Mat tmp(a.n, b.m);//矩阵乘法结果矩阵行数为a的行数，列数为b的列数
    for(int i = 0; i < a.n; i++)
    {
        for(int j = 0; j < b.m; j++)
        {
            for(int k = 0; k < a.m; k++)//a.m == b.n(乘法的前提条件)
            {
                tmp.a[i][j] += (a.a[i][k] * b.a[k][j] % MOD);
                tmp.a[i][j] %= MOD;
            }
        }
    }
    return tmp;
}
Mat pow(Mat a, int n)
{
    Mat tmp(a.n, a.m);
    tmp.init();
    while(n)
    {
        if(n & 1)tmp = mul(tmp, a);
        n /= 2;
        a = mul(a, a);
    }
    return tmp;
}
int c[4][4] =
{
    1,0,1,1,
    1,0,0,0,
    0,1,0,0,
    0,0,1,0,
};
int t[] = {0,2,4,6,9};
int main()
{
    Mat a(4, 4);
    Mat b(4, 1);
    memcpy(a.a, c, sizeof(c));
    for(int i = 0; i < 4; i++)b.a[i][0] = t[4 - i];
    //a.output();
    //b.output();
    int n ,k;
    while(cin >> n >> k)
    {
        MOD = k;
        if(n <= 4)
        {
            cout<<t[n]%k<<endl;
        }
        else
        {
            Mat ans = pow(a, n - 4);
            ans = mul(ans, b);
            //ans.output();
            cout<<ans.a[0][0]<<endl;
        }
    }
}