1、Kruskal算法描述
Kruskal算法是基于贪心的思想得到的。首先我们把所有的边按照权值先从小到大排列,接着按照顺序选取每条边,如果这条边的两个端点不属于同一集合,那么就将它们合并,直到所有的点都属于同一个集合为止。至于怎么合并到一个集合,那么这里我们就可以用到一个工具——-并查集(不知道的同学请移步:Here)。换而言之,Kruskal算法就是基于并查集的贪心算法。
Prim算法适用于稠密图 Kruskal适用于稀疏图
2、Kruskal算法流程
对于图G(V,E),以下是算法描述:
输入: 图G
输出: 图G的最小生成树
具体流程:
(1)将图G看做一个森林,每个顶点为一棵独立的树
(2)将所有的边加入集合S,即一开始S = E
(3)从S中拿出一条最短的边(u,v),如果(u,v)不在同一棵树内,则连接u,v合并这两棵树,同时将(u,v)加入生成树的边集E'
(4)重复(3)直到所有点属于同一棵树,边集E'就是一棵最小生成树
输入: 图G
输出: 图G的最小生成树
具体流程:
(1)将图G看做一个森林,每个顶点为一棵独立的树
(2)将所有的边加入集合S,即一开始S = E
(3)从S中拿出一条最短的边(u,v),如果(u,v)不在同一棵树内,则连接u,v合并这两棵树,同时将(u,v)加入生成树的边集E'
(4)重复(3)直到所有点属于同一棵树,边集E'就是一棵最小生成树
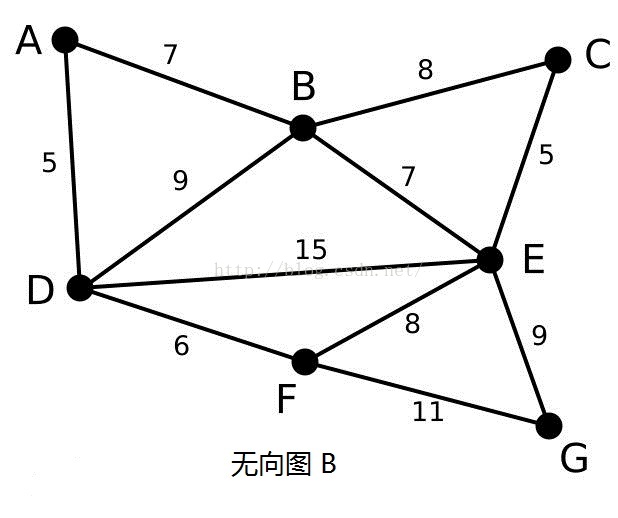
我们用现在来模拟一下Kruskal算法,下面给出一个无向图B,我们使用Kruskal来找无向图B的最小生成树。
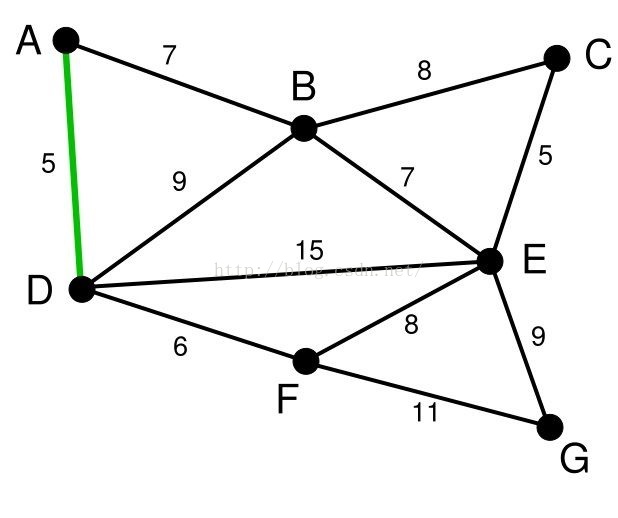
首先,我们将所有的边都进行从小到大的排序。排序之后根据贪心准则,我们选取最小边(A,D)。我们发现顶点A,D不在一棵树上,所以合并顶点A,D所在的树,并将边(A,D)加入边集E‘。
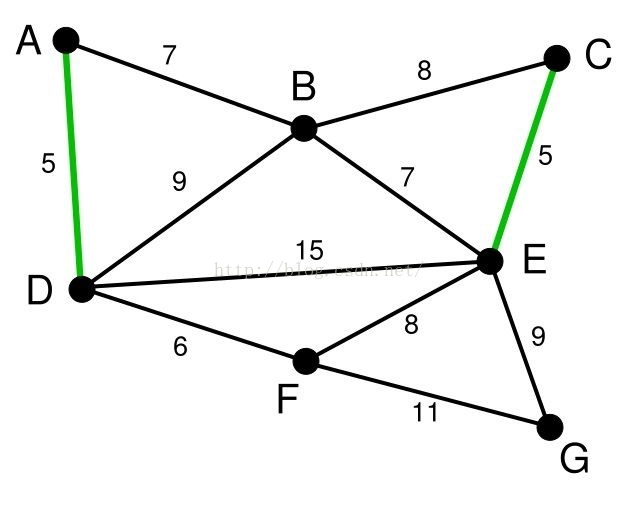
我们接着在剩下的边中查找权值最小的边,于是我们找到的(C,E)。我们可以发现,顶点C,E仍然不在一棵树上,所以我们合并顶点C,E所在的树,并将边(C,E)加入边集E'
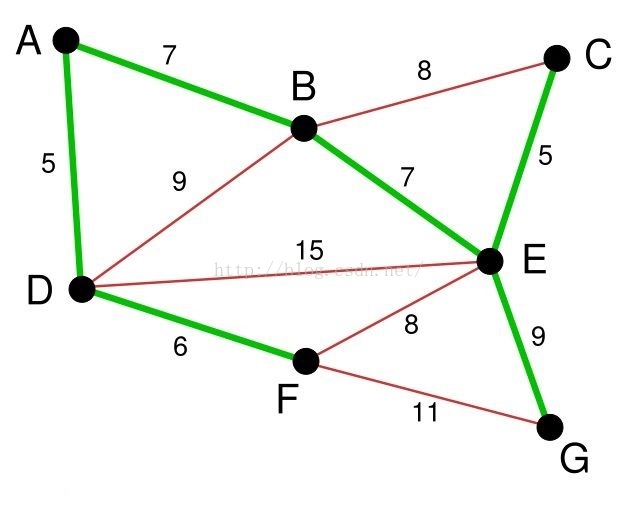
不断重复上述的过程,于是我们就找到了无向图B的最小生成树,如下图所示:
3、Kruskal算法的时间复杂度
Kruskal算法每次要从都要从剩余的边中选取一个最小的边。通常我们要先对边按权值从小到大排序,这一步的时间复杂度为为O(|Elog|E|)。Kruskal算法的实现通常使用并查集,来快速判断两个顶点是否属于同一个集合。最坏的情况可能要枚举完所有的边,此时要循环|E|次,所以这一步的时间复杂度为O(|E|α(V)),其中α为Ackermann函数,其增长非常慢,我们可以视为常数。所以Kruskal算法的时间复杂度为O(|Elog|E|)。
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cmath> 6 #include<queue> 7 #include<stack> 8 #include<map> 9 #include<sstream> 10 using namespace std; 11 typedef long long ll; 12 const int maxn = 3e5 + 10; 13 const int INF = 1 << 30; 14 int dir[4][2] = {1,0,0,1,-1,0,0,-1}; 15 int T, n, m, x; 16 struct edge 17 { 18 int u, v, w; 19 bool operator <(const edge& a)const 20 { 21 return w < a.w; 22 } 23 }; 24 edge a[maxn]; 25 int par[600], high[600]; 26 //初始化n个元素 27 void init(int n) 28 { 29 for(int i = 0; i < n; i++) 30 { 31 par[i] = i; 32 high[i] = 0; 33 } 34 } 35 //查询树的根 36 int Find(int x) 37 { 38 return par[x] == x ? x : par[x] = Find(par[x]);//路径压缩 39 } 40 void unite(int x, int y) 41 { 42 x = Find(x); 43 y = Find(y); 44 if(x == y)return; 45 if(high[x] < high[y])par[x] = y;//y的高度高,将x的父节点设置成y 46 else 47 { 48 par[y] = x; 49 if(high[x] == high[y])high[x]++; 50 } 51 } 52 bool same(int x, int y) 53 { 54 return Find(x) == Find(y); 55 } 56 void kruskal(int n, int m)//点数n,边数m 57 { 58 int sum_mst = 0;//mst权值 59 int num= 0;//已经选择的边的边数 60 sort(a, a + m);//边进行排序 61 init(n);//初始化并查集 62 for(int i = 0; i < m; i++) 63 { 64 int u = a[i].u; 65 int v = a[i].v; 66 if(Find(u - 1) != Find(v - 1))//图最开始的下标是1,并查集是0 67 { 68 printf("%d %d %d ", u, v, a[i].w); 69 sum_mst += a[i].w; 70 num++; 71 unite(u - 1, v - 1); 72 } 73 if(num >= n - 1)break; 74 } 75 printf("weight of mst is %d ", sum_mst); 76 } 77 int main() 78 { 79 cin >> n >> m; 80 for(int i = 0; i < m; i++) 81 { 82 cin >> a[i].u >> a[i].v >> a[i].w; 83 } 84 kruskal(n, m); 85 return 0; 86 } 87 输入: 88 7 9 89 1 2 28 90 1 6 10 91 2 3 16 92 2 7 14 93 3 4 12 94 4 5 22 95 4 7 18 96 5 6 25 97 5 7 24 98 输出: 99 1 6 10 100 3 4 12 101 2 7 14 102 2 3 16 103 4 5 22 104 5 6 25 105 weight of mst is 99