接上文--->【每日算法】C语言8大经典排序算法(1)
二、插入类排序
插入排序(Insertion Sort)的基本思想是:每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子文件中的适当位置,直到全部记录插入完成为止。
插入排序一般意义上有两种:直接插入排序和希尔排序,下面分别介绍。
3、直接插入排序
基本思想:
最基本的操作是将第i个记录插入到前面i-1个以排好序列的记录中。具体过程是:将第i个记录的关键字K依次与其前面的i-1个已经拍好序列的记录进行比较。将所有大于K的记录依次向后移动一个位置,直到遇到一个关键字小于或等于K的记录,此时它后面的位置必定为空,则将K插入。
图示:
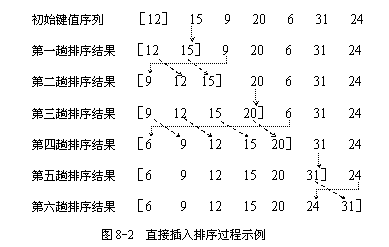

C语言实现:
void InsertSort(int arr[], int n) { int temp; int i,j; for (int i = 1; i < arr.Length; i++)
{
int temp = arr[i];
int j = i;
while ((j > 0) && (arr[j - 1] > t))
{
arr[j] = arr[j - 1];//交换顺序
--j;
}
arr[j] = temp;
} }
算法分析:
1.算法的时间性能分析
对于具有n个记录的文件,要进行n-1趟排序。
各种状态下的时间复杂度:
初始文件状态 正序 反序 无序(平均)
字比较次数 1 i+1 (i-2)/2
总关键字比较次数 n-1 (n+2)(n-1)/2 ≈n2/4
第i趟记录移动次数 0 i+2 (i-2)/2
总的记录移动次数 0 (n-1)(n+4)/2 ≈n2/4
时间复杂度 0(n) O(n2) O(n2)
注意:
初始文件按关键字递增有序,简称"正序"。
初始文件按关键字递减有序,简称"反序"。
2.算法的空间复杂度分析
算法所需的辅助空间是一个监视哨,辅助空间复杂度S(n)=O(1)。是一个就地排序。
3.直接插入排序的稳定性
直接插入排序是稳定的排序方法。
直接插入排序法,针对少量的数据项排序,速度比较快,数据越大,这中方法的劣势也就越明显了。
改进方案:折半插入排序(binary insertion sort)
思路:折半插入排序(binary insertion sort)是对插入排序算法的一种改进,由于排序算法过程中,就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列,这样我们不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度。
具体操作:在将一个新元素插入已排好序的数组的过程中,寻找插入点时,将待插入区域的首元素设置为a[low],末元素设置为a[high],则轮比较时将待插入元素与a[m],其中m=(low+high)/2相比较,如果比参考元素小,则选择a[low]到a[m-1]为新的插入区域(即high=m-1),否则选择a[m+1]到a[high]为新的插入区域(即low=m+1),如此直至low<=high不成立,即将此位置之后所有元素后移一位,并将新元素插入a[high+1]。
C语言实现:
void BInsertSort(int data[],int n) { int low,high,mid; int temp,i,j; for(i=1;i<n;i++) { low=0; temp=data[i];// 保存要插入的元素 high=i-1; while(low<=high) //折半查找到要插入的位置 { mid=(low+high)/2; if(data[mid]>temp) high=mid-1; else low=mid+1; } int j = i; while ((j > low) && (arr[j - 1] > t)) { arr[j] = arr[j - 1];//交换顺序 --j; } arr[low] = temp; } }
算法分析:折半插入排序算法是一种稳定的排序算法,比直接插入算法明显减少了关键字之间比较的次数,因此速度比直接插入排序算法快,但记录移动的次数没有变,所以折半插入排序算法的时间复杂度仍然为O(n^2),与直接插入排序算法相同。附加空间O(1)。
4、希尔排序
希尔排序(Shell Sort)是插入排序的一种。是针对直接插入排序算法的改进。该方法又称缩小增量排序,因DL.Shell于1959年提出而得名。
基本思想:
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分成d1个组。所有距离为dl的倍数的记录放在同一个组中。先在各组内进行直接插人排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量dt=1(dt<dt-l<…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。
该方法实质上是一种分组插入方法。
举例阐述:
例如,假设有这样一组数[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ],如果我们以步长为5开始进行排序,我们可以通过将这列表放在有5列的表中来更好地描述算法,这样他们就应该看起来是这样:
13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10
然后我们对每列进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
将上述四行数字,依序接在一起时我们得到:[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ].这时10已经移至正确位置了,然后再以3为步长进行排序:
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45
排序之后变为:
10 14 13 25 23 33 27 25 59 39 65 73 45 94 82 94
最后以1步长进行排序(此时就是简单的插入排序了)。
图示:
C++代码实现:
1 void shellsort(int *data, size_t size) 2 { 3 for (int gap = size / 2; gap > 0; gap /= 2) 4 for (int i = gap; i < size; ++i) 5 { 6 7 int key = data[i]; 8 int j = 0; 9 for( j = i -gap; j >= 0 && data[j] > key; j -=gap) 10 { 11 data[j+gap] = data[j]; 12 } 13 data[j+gap] = key; 14 } 15 }
性能分析:
希尔排序是按照不同步长对元素进行插入排序,当刚开始元素很无序的时候,步长最大,所以插入排序的元素个数很少,速度很快;当元素基本有序了,步长很小,插入排序对于有序的序列效率很高。所以,希尔排序的时间复杂度会比o(n^2)好一些。由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。
| 最差时间复杂度 | 根据步长序列的不同而不同。 已知最好的: 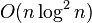 |
|---|---|
| 最优时间复杂度 | O(n) |
| 平均时间复杂度 | 根据步长序列的不同而不同。 |