1.阅读并运行示例PassArray.java,观察并分析程序输出的结果,小结,然后与下页幻灯片所讲的内容进行对照。
按引用传递与按值传送数组类型方法参数的最大关键在于:
使用前者时,如果方法中有代码更改了数组元素的值,实际上是直接修改了原始的数组元素。
使用后者则没有这个问题,方法体中修改的仅是原始数组元素的一个拷贝。
2.阅读QiPan.java示例程序了解如何利用二维数组和循环语句绘制五子棋盘。
package T6;
import java.io.*;
public class Qipan {
private String[][] pan = new String[15][15];//定义棋盘及大小
public void initpan()//初始化
{
for(int i = 0; i < 15; i++)
for(int j = 0; j < 15; j++)
pan[i][j] = "╋";
}
public void show()//棋盘输出
{
for(int i = 0; i < 15; i++)
{
for(int j = 0; j < 15; j++)
System.out.print(pan[i][j]);
System.out.println();
}
}
public static void main(String[] args)throws Exception
{
Qipan qp = new Qipan();
qp.initpan();
qp.show();
//这是用于获取键盘输入的方法
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String inputStr = null;
System.out.println("请输入您下棋的座标,应以x,y的格式:");
while ((inputStr = br.readLine()) != null)
{
//将用户输入的字符串以逗号(,)作为分隔符,分隔成2个字符串
String[] posStrArr = inputStr.split(",");
//将2个字符串转换成用户下棋的座标
int xPos = Integer.parseInt(posStrArr[0]);
int yPos = Integer.parseInt(posStrArr[1]);
//把对应的数组元素赋为"●"。
qp.pan[xPos - 1][yPos - 1] = "●";
/*
电脑随机生成2个整数,作为电脑下棋的座标,赋给board数组。
还涉及
1.座标的有效性,只能是数字,不能超出棋盘范围
2.如果下的棋的点,不能重复下棋。
3.每次下棋后,需要扫描谁赢了
*/
qp.show();
System.out.println("请输入您下棋的座标,应以x,y的格式:");
}
}
}
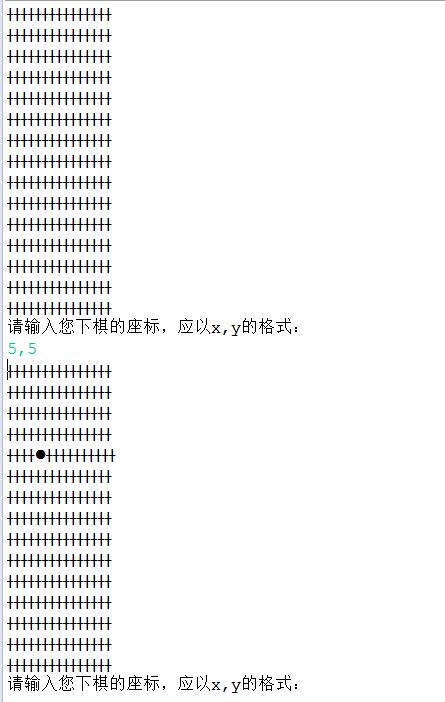
程序中定义数组,初始化数组,只能实现自己下棋,不能实现人机对弈。
3.
请编写一个程序将一个整数转换为汉字读法字符串。比如“1123”转换为“一千一百二十三”。
源代码:
package T6;
//胡建峰,2016.11.02
//整数转化为汉字表达
import java.util.Scanner;
public class Hanzi
{
private String[] han = {"零" , "壹" , "贰" , "叁" , "肆" , "伍" , "陆" , "柒" , "捌" , "玖"};//数字汉字数组
private String[] unit = {"十" , "百" , "千" , "万" , "十万" , "百万"};//单位汉字数组
private String change(int n) {
String result = "";//输出
String num = String.valueOf(n);//n转化为string
int length = num.length();//长度
for(int i = 0; i < length; i ++)//添加汉字及单位,对0特殊
{
int x = num.charAt(i) - '0';
if(x != 0)
{
if(i != length - 1)
{
result += han[x];
result += unit[length - i - 2];
}
else
result += han[x];
}
else
{
if(length == 1)
result += han[0];
else if(result.charAt(result.length() - 1) != '零')
result += han[0];
}
}
if(result.length() == 1)
return result;
else if(result.charAt(result.length() - 1) == '零')
return result.substring(0, result.length() - 1);
else
return result;
}
public static void main(String[] args) {
System.out.print("请输入一个整数(最多六位数):");//输入
Scanner s = new Scanner(System.in);
int num = s.nextInt();
s.close();
Hanzi hz = new Hanzi();
System.out.println("转化为汉字表达为:" + hz.change(num));//输出
}
}
运行结果:



多次测试可以实现六位数字的转化。
更进一步,能否将数字表示的金额改为“汉字表达? 比如将“¥123.52”转换为“壹佰贰拾叁元伍角贰分”。
源码:
package T6;
//胡建峰,2016.11.06
//整数转化为汉字表达
import java.util.Scanner;
public class Hanzi2 {
private String[] han = {"零" , "壹" , "贰" , "叁" , "肆" , "伍" , "陆" , "柒" , "捌" , "玖"};//数字汉字数组
private String[] unit = {"十" , "百" , "千" , "万" , "十万" , "百万"};//单位汉字数组
private String change(double n) {
String result = "";//输出
String num = String.valueOf(n);//n转化为string
int length = num.indexOf(".");//长度
int len = num.length();
for(int i = 0; i < length; i ++)//添加汉字及单位,对0特殊
{
int x = num.charAt(i) - '0';
if(x != 0)
{
if(i != length - 1)
{
result += han[x];
result += unit[length - i - 2];
}
else
result += han[x];
}
else
{
if(length == 1)
result += han[0];
else if(result.charAt(result.length() - 1) != '零')
result += han[0];
}
}
if(result.charAt(result.length() - 1) == '零')//为.前加元
result = result.substring(0, result.length() - 1) + "元";
else
result += "元";
//小数转化
for(int j = length + 1; j < len; j++)
{
int y = num.charAt(j) - '0';
if(j == length + 1)
{
if(y != 0)
result += (han[y] + "角");
else if(len - j == 2)
result += "零";
}
else
{
if(y != 0)
result += (han[y] + "分");
}
}
return result;//结果输出
}
public static void main(String[] args) {
System.out.print("请输入一个钱数(最多六位数):");//输入
Scanner s = new Scanner(System.in);
double num = s.nextDouble();
s.close();
Hanzi2 hz = new Hanzi2();
System.out.println("转化为汉字表达为:" + hz.change(num));//输出
}
}
结果截图:



对小数点前的转化后加个元,再对小数点后的判断。
4.

(1)
源代码:
package T6;
//胡建峰,2016.11.06
//大数运算
import java.util.Scanner;
public class Bigint {
private int [] big = new int[20];
public void init()
{
for(int i = 0; i < 20; i++)
big[i] = 0;
}
public void input(String s)
{
for(int i = 0 ; i < s.length(); i++)
big[s.length() - i - 1] = s.charAt(i) - '0';
}
public void show()
{
int al = 0;
for(int i = 19;i >= 0 ; i--)
if(big[i] != 0)
{
al = i;
break;
}
for(int j = 0;j <= al; j++)
System.out.print(big[al - j]);
}
public boolean bigger(Bigint a,Bigint b)
{
int al = 0,bl = 0;
for(int i = 19;i >= 0 ; i--)
if(a.big[i] != 0)
{
al = i;
break;
}
for(int i = 19;i >= 0 ; i--)
if(b.big[i] != 0)
{
bl = i;
break;
}
if(al > bl)
return true;
else if(al < bl)
return false;
else
{
if(a.big[al] > b.big[al])
return true;
else if(a.big[al] < b.big[al])
return false;
else
{
while(a.big[al] == b.big[al])
{
if(al != 0)
{
if(a.big[al - 1] > b.big[al - 1])
return true;
else if(a.big[al - 1] < b.big[al - 1])
return false;
else
al --;
}
else
return true;
}
}
}
return false;
}
public void add(Bigint a,Bigint b)
{
Bigint result = new Bigint();
result.init();
if(a.bigger(a, b))
{
int l = 0,temp;
for(int i = 19;i >= 0 ; i--)
if(a.big[i] != 0)
{
l = i;
break;
}
l++;
for(int j = 0;j < l; j++)
{
temp = a.big[j] + b.big[j];
if(temp > 9)
{
result.big[j] = (temp - 10);
result.big[j + 1] += 1;
}
else
result.big[j] = temp;
}
}
else
{
int l = 0,temp;
for(int i = 19;i >= 0 ; i--)
if(b.big[i] != 0)
{
l = i;
break;
}
l++;
for(int j = 0;j < l; j++)
{
temp = a.big[j] + b.big[j];
if(temp > 9)
{
result.big[j] = (temp - 10);
result.big[j + 1] += 1;
}
else
result.big[j] = temp;
}
}
result.show();
System.out.print("
");
}
public void sub(Bigint a,Bigint b)
{
Bigint result = new Bigint();
result.init();
if(a.bigger(a, b))
{
int l = 0,temp;
for(int i = 19;i >= 0 ; i--)
if(a.big[i] != 0)
{
l = i;
break;
}
for(int j = 0;j < l; j++)
{
temp = a.big[j] - b.big[j];
if(temp < 0)
{
result.big[j] = (temp + 10);
result.big[j + 1] -= 1;
}
else
result.big[j] = temp;
}
}
else
{
System.out.print("-");
int l = 0,temp;
for(int i = 19;i >= 0 ; i--)
if(b.big[i] != 0)
{
l = i;
break;
}
for(int j = 0;j < l; j++)
{
temp = a.big[j] - b.big[j];
if(temp < 0)
{
result.big[j] = (temp + 10);
result.big[j + 1] -= 1;
}
else
result.big[j] = temp;
}
}
result.show();
System.out.print("
");
}
public static void main(String[] args) {
Bigint b1 = new Bigint();
b1.init();
Bigint b2 = new Bigint();
b2.init();
System.out.println("请输入两个正的大数:");
Scanner s = new Scanner(System.in);
String str1 = s.next();
String str2 = s.next();
s.close();
b1.input(str1);
b2.input(str2);
System.out.print(str1 + "+" + str2 + "=");
b1.add(b1, b2);
System.out.print(str1 + "-" + str2 + "=");
b1.sub(b1, b2);
}
}
结果截图:
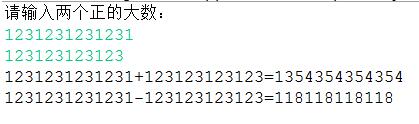
小结:通过定义int数组来实现大数相加相减,初始化,输入后将数字反过来存,然后加法是比较大小,补0,然后每位相加,大于9的进1,最后再反过来输出。减法为小于0的,上一位减1。
(2)其实要实现大整数类也不难,简单一想,我们可以把一个很大很长的数分成多个短小的数,然后保存在一个数组中,大数之间的四则运算及其它运算都是通过数组完成.JDK就是这么实现的.JDK的BigInteger类里用一个int数组来保存数据。
分析该构造函数源码之前,先想一个问题,构造一个大整数开始最主要的问题是如何把一个大数保存到mag数组中,通常我们自己实现的话很有可能是数组每块存一位数(假设大数为10进制),但这样的话想想也知道太浪费空间,因为一个int值可以保存远不止一位十进制数. Java语言里每个int值大小范围是-2^31至2^31-1 即-2147483648~2147483647,因此一个int值最多可保存一个10位十进制的整数,但是为了防止超出范围(2222222222这样的数int已经无法存储),保险的方式就是每个int保存9位的十进制整数.JDK里的mag数组即是这样的保存方式.因此若一串数为:18927348347389543834934878. 划分之后就为:18927348 | 347389543 | 834934878. mag[0]保存18927348 ,mag[1]保存347389543 ,mag[2]保存834934878. 这样划分可以最大利用每一个int值,使得mag数组占用更小的空间.当然这只是第一步. 划分的问题还没有说完,上述构造函数能够支持不同进制的数,最终转换到mag数组里面的数都是十进制,那么不同进制的大数,每次选择划分的位数就不相同,若是2进制,每次就可以选择30位来存储到一个int数中(int值大小范围是-2^31至2^31-1),若是3进制3^19<2147483647<3^20,因此每次就可以选择19位来存储到一个int数中,对于不同进制每次选择的位数不同,因此需要有一个数组来保存不同进制应当选择的位数。
bitsPerDigit是用于计算radix进制m个有效数字 转换成2进制所需bit位[假设所需x位],我们来看一个计算式:radix^m - 1 = 2^x - 1, 解这个方程得 x = m * log2(radix) , 现在m是几位有效数字,常量就只有 log2(radix),这是一个小数,这不是我们喜欢的,所以我们希望用一个整数来表示,于是我们把他扩大1024倍然后取整,例如3进制 bitsPerDigit[3] = 1624(我用计算器算了一下 x = log2(3) * 1024 ~= 1623.xxx) ,我们队这个数取整,为什么取1624呢,其实只要不超过太多都可以的,你可以设置为1620,1600,1610...;”
(3)
乘法代码:
public static String multiply(String x, String y){
if(isNullAndNotNumber(x,y)){
return null;
}
if(x.equals("0") || y.equals("0")){
return "0";
}
int[] a = toIntArray(x);
int[] b = toIntArray(y);
int[] temp1 = null;
int[] temp2 = null;
int enter = 0;
int result = 0;
int count = 1;
for(int i=(b.length -1); i>=0; i--){
temp1 = new int[a.length+(++count)];
enter = 0;
for(int j=a.length-1; j>=0; j--){
result = a[j]*b[i]+enter;
temp1[j+2] = result;
enter = result/10;
}
temp1[1] = enter;
temp1[0] = 0;
temp2 = addIntArray(temp1, temp2);
}
StringBuffer sb = new StringBuffer(32);
for(int j=0; j<temp2.length; j++){
if(temp2[j] == 0 && sb.length() == 0){
continue;
} else {
sb.append(temp2[j]);
}
}
return sb.toString();
}
除法代码:
public static List<String> divide(String x, String y) {
if(isNullAndNotNumber(x,y)){
return null;
}
List<String> returnList = new ArrayList<String>();
if(y.equals("0") || x.equals("0")){
returnList.add("0");
returnList.add("0");
return returnList;
}
String quotient = "";//quotient
String remainder = "";//remainder
if (isBig(x, y) == false) {
remainder = y;
quotient = "0";
returnList.add(quotient);
returnList.add(remainder);
return returnList;
}
int i = y.length();
remainder = x.substring(0, i);
do {
for (int j = 9; j >= 1; j--) {
if ((isBig(remainder, multiply(y, Integer.valueOf(j).toString())) == false) && (isBig(remainder, multiply(y, Integer.valueOf(j - 1).toString())) == true)) {
if((j-1) > 0){
quotient += (j-1);
}
remainder = subtract(remainder, multiply(y, Integer.valueOf(j-1).toString()));
break;
}
}
int len = remainder.length();
for (int k = 0; (k < y.length() - len) && (i < x.length()); k++) {
remainder += x.charAt(i);
i++;
if (isBig(remainder, y) == false) {
quotient += "0";
}
}
if ((isBig(remainder, y) == false) && (i < x.length())) {
remainder += x.charAt(i);
i++;
}
} while (i < x.length());
for (int j = 9; j >= 1; j--) {
if ((isBig(remainder, multiply(y, Integer.valueOf(j).toString())) == false) && (isBig(remainder, multiply(y, Integer.valueOf(j - 1).toString())) == true)) {
if((j-1) > 0){
quotient += (j-1);
}
remainder = subtract(remainder, multiply(y, Integer.valueOf(j-1).toString()));
break;
}
}
returnList.add(quotient);
returnList.add(remainder);
return returnList;
}
阶乘为一个乘法递归算法。
小结:在网上查到了算法,但是还没有添加至我的算法中,后我会修改。
课后作业:
1.设计思路:定义一个输出结果和一个数组,初始化数组的时候为数组赋随机值,同时求和,然后用窗口输出结果。最后美化一下输出。
2.程序流程图:
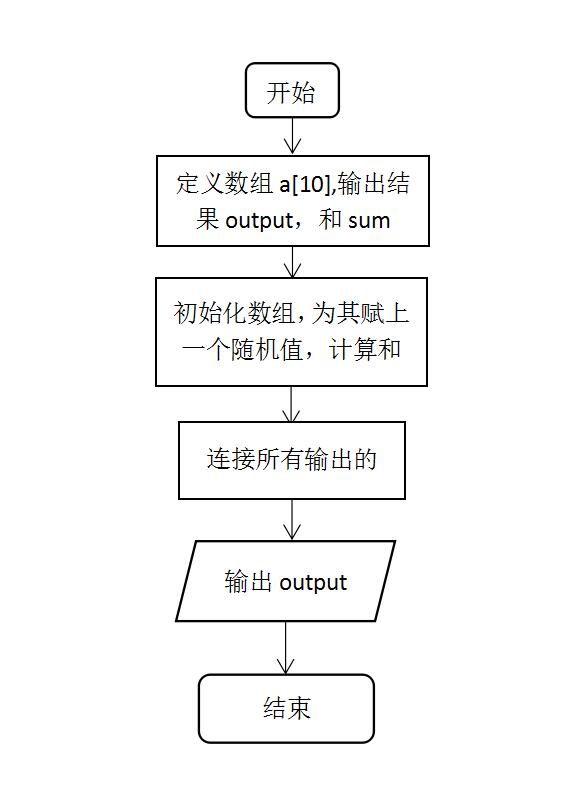
3.源程序代码:
package T6;
import java.util.Random;
//胡建峰,2016.11.2
//随机生成10个数,求和(数组)
import javax.swing.*;
public class RandomSum {
public static void main(String[] args) {
String output="数组元素为:
";//定义输出
int sum = 0;
int a[] = new int[10];//数组
for(int i = 0; i < 10; i++ )//生成1-100的随机数赋给数组,添加输出和计算和
{
a[i] = new Random().nextInt(99)+1;
output += (a[i] + " ");
sum += a[i];
if((i + 1) % 2 == 0)
output += "
";
}
output += ("数组和为:" + sum); //输出和
JTextArea outputArea = new JTextArea( 8, 10 );//输出消息框
outputArea.setText( output );
JOptionPane.showMessageDialog( null, outputArea,
"result", JOptionPane.PLAIN_MESSAGE );
System.exit( 0 );
}
}
4.结果截图:
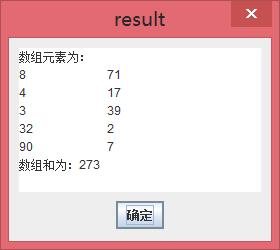
5.总结:
在使用数组时必须在主函数中对其初始化,其他操作注意下就可以了。