一、啤酒和饮料
啤酒每罐2.3元,饮料每罐1.9元。小明买了若干啤酒和饮料,一共花了82.3元。
我们还知道他买的啤酒比饮料的数量少,请你计算他买了几罐啤酒。
注意:答案是一个整数。请通过浏览器提交答案。
不要书写任何多余的内容(例如:写了饮料的数量,添加说明文字等)。
思路:暴力。
答案:11。
#include <stdio.h>
double a=2.3,b=1.9,f;
int main()
{
for(double i=0;;i++) //啤酒·
{
for(double j=i+1;i*a+j*b<=82.30;j++) //饮料.
{
double t=i*a+j*b;
if(t==82.30)
{
f=1;
printf("%.0lf",i);
break;
}
}
if(f) break;
}
return 0;
}
二、切面条
一根高筋拉面,中间切一刀,可以得到2根面条。
如果先对折1次,中间切一刀,可以得到3根面条。
如果连续对折2次,中间切一刀,可以得到5根面条。
那么,连续对折10次,中间切一刀,会得到多少面条呢?
答案是个整数,请通过浏览器提交答案。不要填写任何多余的内容。
思路:很容易发现,规律 f[n]=2*f[n-1]-1。因此我们可以通过循环计算出答案。
答案 :1025.
#include <stdio.h>
int main()
{
long long f[11];
f[0]=2;
for(int i=1;i<=10;i++)
f[i]=2*f[i-1]-1;
printf("%lld",f[10]);
return 0;
}
三、李白打酒
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店5次,遇到花10次,已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白遇到店和花的次序,可以把遇店记为a,遇花记为b。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
注意:通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。
思路:深搜 。统计一下符合条件的情况即可。
答案:14 。
#include <stdio.h>
int a[20],ans;
void dfs(int x)
{
if(x==14)
{
int f=0;
int s=2,p=0,q=0;
for(int i=0;i<14;i++)
{
if(a[i]) //店
{
p++;
s*=2;
}
else //花
{
q++;
s--;
}
if(s<0)
{
f=1;
break;
}
}
if(!f&&s==1&&p==5&&q==9) // 最后一个是花
{
ans++;
}
return ;
}
dfs(x+1); //花
a[x]=1;
dfs(x+1); //店
a[x]=0;
}
int main()
{
dfs(0);
printf("%d",ans);
return 0;
}
六、奇怪的分式
上小学的时候,小明经常自己发明新算法。一次,老师出的题目是:
1/4 乘以 8/5
小明居然把分子拼接在一起,分母拼接在一起,答案是:18/45 (参见图1.png)

老师刚想批评他,转念一想,这个答案凑巧也对啊,真是见鬼!
对于分子、分母都是 1~9 中的一位数的情况,还有哪些算式可以这样计算呢?
请写出所有不同算式的个数(包括题中举例的)。
显然,交换分子分母后,例如:4/1 乘以 5/8 是满足要求的,这算做不同的算式。
但对于分子分母相同的情况,2/2 乘以 3/3 这样的类型太多了,不在计数之列!
注意:答案是个整数(考虑对称性,肯定是偶数)。请通过浏览器提交。不要书写多余的内容。
答案:14.
思路:还是暴力。。。。
#include <stdio.h>
long long ans;
int main()
{
for(int a=1;a<10;a++) //分子
{
for(int b=1;b<10;b++)//分子
{
for(int c=1;c<10;c++)//分母
{
for(int d=1;d<10;d++)//分母
{
int t1=a*b*(c*10+d);
int t2=c*d*(a*10+b);
//printf("%d %d
",t1,t2);
if(t1==t2&&a!=c&&b!=d)
{
ans++;
}
}
}
}
}
printf("%lld",ans);
return 0;
}
七、六角填数
如图所示六角形中,填入1~12的数字。
使得每条直线上的数字之和都相同。
图中,已经替你填好了3个数字,请你计算星号位置所代表的数字是多少?
请通过浏览器提交答案,不要填写多余的内容
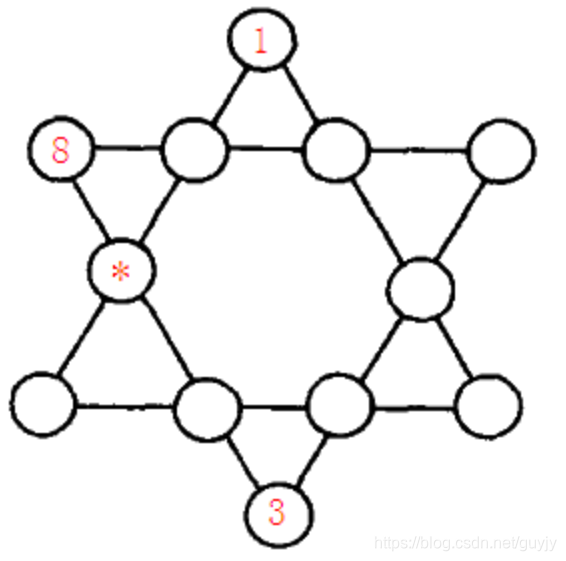
思路:暴力。。。。
答案:10.
#include <stdio.h>
int a[12],b[20],c[6],f;
void dfs(int x) // 放入了x个数
{
if(x==12)
{
f=0;
c[0]=a[0]+a[2]+a[5]+a[7];
c[1]=a[0]+a[3]+a[6]+a[10];
c[2]=a[1]+a[2]+a[3]+a[4];
c[3]=a[1]+a[5]+a[8]+a[11];
c[4]=a[4]+a[6]+a[9]+a[11];
c[5]=a[7]+a[8]+a[9]+a[10];
for(int i=0;i<=5;i++)
{
for(int j=i+1;j<=5;j++)
{
if(c[i]!=c[j])
{
f=1;
break;
}
}
if(f)
{
break;
}
}
if(!f)
{
printf("%d",a[5]);
}
return ;
}
if(x==0)
{
a[x]=1;
dfs(x+1);
return ;
}
if(x==1)
{
a[x]=8;
dfs(x+1);
return ;
}
if(x==11)
{
a[x]=3;
dfs(x+1);
return ;
}
for(int i=1;i<=12;i++)
{
if(i!=1&&i!=3&&i!=8)
{
if(!b[i])
{
b[i]=1;
a[x]=i;
dfs(x+1);
b[i]=0;
}
}
}
}
int main()
{
dfs(0);
return 0;
}
8.标题:蚂蚁感冒
长100厘米的细长直杆子上有n只蚂蚁。它们的头有的朝左,有的朝右。
每只蚂蚁都只能沿着杆子向前爬,速度是1厘米/秒。
当两只蚂蚁碰面时,它们会同时掉头往相反的方向爬行。
这些蚂蚁中,有1只蚂蚁感冒了。并且在和其它蚂蚁碰面时,会把感冒传染给碰到的蚂蚁。
请你计算,当所有蚂蚁都爬离杆子时,有多少只蚂蚁患上了感冒。
【数据格式】
第一行输入一个整数n (1 < n < 50), 表示蚂蚁的总数。
接着的一行是n个用空格分开的整数 Xi (-100 < Xi < 100), Xi的绝对值,表示蚂蚁离开杆子左边端点的距离。正值表示头朝右,负值表示头朝左,数据中不会出现0值,也不会出现两只蚂蚁占用同一位置。其中,第一个数据代表的蚂蚁感冒了。
要求输出1个整数,表示最后感冒蚂蚁的数目。
例如,输入:
3
5 -2 8
程序应输出:
1
再例如,输入:
5
-10 8 -20 12 25
程序应输出:
3
————————————————
思路:这是一道思维题,因为蚂蚁们的相对速度不变,我们可以将蚂蚁掉头理解为蚂蚁相互擦肩而过。。。这样一来,从第一只蚂蚁开始看,统计所有会被感染的蚂蚁。
#include <stdio.h>
int ans,n,m,t,f,z,y;
int main()
{
scanf("%d",&n);
scanf("%d",&t); //第一只蚂蚁
for(int i=0;i<n-1;i++)
{
if(t>0) //第一只蚂蚁向右走
{
scanf("%d",&m);
if(m>0&&m<t) //向右走并且在第一只蚂蚁左边
{
y++;
}
else if(m<0&&(-m)>t) //向左走并且在第一只蚂蚁右边
{
z++;
f=1;
}
}
else //第一只蚂蚁向左走
{
scanf("%d",&m);
if(m>0&&m<(-t)) //向右走并且在第一只蚂蚁左边
{
y++;
f=1;
}
else if(m<0&&(-m)>(-t))//向左走并且在第一只蚂蚁右边
{
z++;
}
}
if(f)
{
ans=z+y+1;
}
else
{
ans=1;
}
}
printf("%d",ans);
return 0;
}
9.标题:地宫取宝
X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。 地宫的入口在左上角,出口在右下角。 小明被带到地宫的入口,国王要求他只能向右或向下行走。 走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。当小明走到出口时,如果他手中的宝贝恰好是k件,则这些宝贝就可以送给小明。
请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这k件宝贝。
【数据格式】
输入一行3个整数,用空格分开:n m k (1<=n,m<=50, 1<=k<=12)
接下来有 n 行数据,每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值
要求输出一个整数,表示正好取k个宝贝的行动方案数。该数字可能很大,输出它对 1000000007 取模的结果。
例如,输入:
2 2 2
1 2
2 1
程序应该输出:
2
再例如,输入:
2 3 2
1 2 3
2 1 5
程序应该输出:
14
————————————————
思路:记忆化搜索。这题用dfs爆搜的话会超时,所以我们采用记忆化搜索。
先贴一下百度上的名词解释:
记忆化搜索:算法上依然是搜索的流程,但是搜索到的一些解用动态规划的那种思想和模式作一些保存。
一般说来,动态规划总要遍历所有的状态,而搜索可以排除一些无效状态。
更重要的是搜索还可以剪枝,可能剪去大量不必要的状态,因此在空间开销上往往比动态规划要低很多。
记忆化算法在求解的时候还是按着自顶向下的顺序,但是每求解一个状态,就将它的解保存下来,
以后再次遇到这个状态的时候,就不必重新求解了。
这种方法综合了搜索和动态规划两方面的优点,因而还是很有实用价值的。
代码:
#include <stdio.h>
#include <string.h>
long long n,m,k,mod=1e9+7,map[55][55],dp[55][55][35][15]; //dp[x][y][num][max]表示在(x,y)我们有num件物品且最大值是max时到终点的方案数
long long dfs(long long x,long long y,long long num,long long max)
{
if(dp[x][y][num][max+1]!=-1) //题意说明最小的价值为0,所以我们初始化max为-1 ,在数组中保证下标非负
{
return dp[x][y][num][max+1];//返回此状态到终点的方案数
}
if(x==n&&y==m)
{
if(k==num||(k-1==num&&map[x][y]>max)) //此时已经恰好k件或者能取终点
{
return dp[x][y][num][max+1]=1; //表示有一条路
}
else
{
return dp[x][y][num][max+1]=0;//此状态无符合条件的路到终点
}
}
long long s=0;//定义为局部变量
if(x+1<=n)
{
if(map[x][y]>max)
s+=dfs(x+1,y,num+1,map[x][y]);
s+=dfs(x+1,y,num,max);
}
if(y+1<=m)
{
if(map[x][y]>max)
s+=dfs(x,y+1,num+1,map[x][y]);
s+=dfs(x,y+1,num,max);
}
return dp[x][y][num][max+1]=s%mod;
}
int main()
{
scanf("%lld%lld%lld",&n,&m,&k);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
scanf("%lld",&map[i][j]);
}
}
memset(dp,-1,sizeof(dp));
printf("%lld",dfs(1,1,0,-1));
return 0;
}