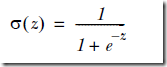Machine Learning in Action -- Logistic regression

这个系列，重点关注如何实现，至于算法基础，参考Andrew的公开课

相较于线性回归，logistic回归更适合用于分类

因为他使用Sigmoid函数，因为分类的取值是0，1

对于分类，最完美和自然的函数，当然是Heaviside step function，即0-1阶跃函数，但是这个函数中数学上有时候比较难处理

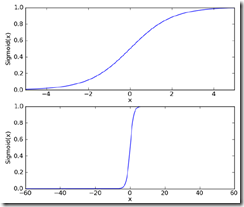
所以用Sigmoid函数来近似模拟阶跃函数，

可以看到Sigmoid在增大坐标尺度后，已经比较接近于阶跃函数

其中，

而logistic回归就是要根据训练集找到，最优的w向量

下面就通过源码来看看如何用梯度下降来解logistic问题，

def loadDataSet():
    dataMat = []; labelMat = []  #数组
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])]) #加入一个数据点，其中‘1.0’代表截距
        labelMat.append(int(lineArr[2])) #每个数据点的lable，用于训练
    return dataMat,labelMat

def sigmoid(inX):
    return 1.0/(1+exp(-inX))

def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)  #首先将array转换为matrix
    labelMat = mat(classLabels).transpose()  #将lables转秩，因为一个lable对应于dataMatrix中的一行，即一个数据点
    m,n = shape(dataMatrix)
    alpha = 0.001   #学习率
    maxCycles = 500  #迭代次数
    weights = ones((n,1))   #初始化weights向量
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)  #这里是矩阵计算，最终h是个列向量，表示每个数据点的预估值
        error = (labelMat - h)  #和真实值比较，算出error列向量
        weights = weights + alpha * dataMatrix.transpose()* error #这个公式是通过梯度下降推导出来的
    return weights #获得最终的weights参数

这里需要注意，numpy支持矩阵计算，所以

h = sigmoid(dataMatrix*weights)， 其实是完成n×m矩阵和n×1矩阵乘，然后执行n次sigmoid，得到h列向量

至于那个公式，是由于由梯度下降求出的weight迭代公式如下，

得到weights后，进行predict很容易，直接把数据点和weights代入sigmoid函数算出h，以0.5为界近似成0或1

这种原始的梯度下降算法的问题，就是计算量比较大，对于每个weight的迭代都需要遍历数据集一遍，所以如果weight和数据集比较大，很低效

 

stochastic gradient ascent

对于随机梯度下降，每次只用一个数据点来迭代weights

def stocGradAscent0(dataMatrix, classLabels):
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights)) #只取一个数据点
        error = classLabels[i] - h
        weights = weights + alpha * error * dataMatrix[i]
    return weights

但这个简单的随机算法有些问题，

首先只迭代训练集一遍，很可能没有达到收敛，所以准确率不够
其次，每次是依次选取数据点，所以weights会产生周期性的波动
最后，收敛速度不够

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m,n = shape(dataMatrix)
    weights = ones(n)
    for j in range(numIter):  #增加迭代次数
        for i in range(m):
            alpha = 4/(1.0+j+i)+0.01   #动态改变学习率
            randIndex = int(random.uniform(0,len(dataIndex))) #随机选取数据点
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

对于动态改变学习率，
可以看到，学习率会随着迭代次数变大，不断变小，但不会为0，因为有常数项，可以缓解数据波动，并保持多次迭代后仍然对数据有一定的影响
并且当i>>j时，学习略随着迭代次数增加，也不是严格下降的

而随机选取数据点，用于解决周期性波动问题