摘要
(点题)Query optimizers depend on selectivity estimates of query predicates to produce a good execution plan.
(当前的方案)When a query contains multiple predicates, today's optimizers use a variety of(various) assumptions, such as independence between predicates, to estimate selectivity.
While such techniques have the benefit of fast estimation and small memory footprint, they often incur large selectivity estimation errors.
(提出新的方案)In this work, we reconsider selectivity estimation as a regression problem.
We explore application of neural networks and tree-based ensembles to the important problem of selectivity estimation of multi-dimensional range predicates.
(两个设计选择)While their straightforward application does not outperform even simple baselines, we propose two simple yet effective design choices,
i.e., regression label transformation and feature engineering, motivated by the selectivity estimation context.
(实验验证)Through extensive empirical evaluation across a variety of datasets, we show that the proposed models deliver both highly accurate estimates as well as fast estimation.
Introduction
(需求,快,准,低资源占用)Query optimizers use selectivity estimates to identify a good execution plan.
Ideally, a selectivity estimation technique should provide accurate and fast estimates, and use a data structure that has small memory footprint and is effcient to construct and maintain [19].
The requirement of fast estimation follows from the expectation that query optimization time should be small [13, 7], and is an important practical constraint in database systems.
(业界方案,histogram或sampling)To elaborate(详细描述), current database systems primarily use histograms for selectivity estimation of predicates on single table attributes [5, 7].
For multi-dimensional predicates, the default method to calculate combined selectivity is based on a heuristic assumption such as attribute value independence (AVI) [4, 5, 7].
When attributes are correlated, estimates based on such assumptions may lead to huge errors resulting in low quality plans [27, 32].
Some database systems also provide an option for a small data sample [7].
While sampling can capture attribute correlations well, small samples have bad accuracy for selective predicates [34].
Nevertheless, database systems use such methods as they support fast selectivity estimation, e.g., multi-dimensional estimation based on AVI takes < 100sec [38].
(研究领域针对多列SE问题,只能在accuracy和overhead之间tradeoff)
The research community has been actively working on the multi-dimensional selectivity estimation problem [19] leading to many variants of multi-dimensional histograms [12, 21, 38], techniques
that use random samples [22], or use both histograms and samples [34], Section 8 provides a review of related work.
They improve accuracy at the cost of significant increase in space or time overhead, because they fundamentally rely on more histogram buckets or larger samples to capture the data distribution in a high-dimensional space.
(自适应的histogram)Query-driven (self tuning) histograms [40, 10, 12, 22] use more histogram buckets in the subspace that is relevant for the current query workload, to improve the accuracy-cost trade-off in a targeted fashion.
The accuracy of such techniques can degrade when workload queries have more intersections with each other and they spread across a large fraction of high-dimensional space.
(通过分析和实验表明当前的histogram方式效果不行)
We analyzed estimates based on both kinds of histogram techniques:
(i) AVI assumption, that uses only one dimensional histograms; (ii) STHoles [12], that uses a query driven multi-dimensional histogram.
For this experiment, we used a representative real world dataset and a set of queries distributed all over the domain space.......
(SE可以作为一种回归问题,之前的没有类似的尝试)
In addition to above approaches, selectivity estimation has also been formulated as a regression problem:
Given a set of queries labeled with actual selectivity values, learn a function from a query to its selectivity".
Such labeled queries can be collected as feedback from prior query executions [40, 14], as proposed by self-tuning approaches;
or they can be generated online in a data-driven fashion, similar to histogram construction (see Section 6).
Past attempts with regression formulation typically employed neural networks [11, 26, 29, 28, 25].
These methods are not designed for fast estimation of multi-dimensional range selectivity.
Contribution
Regression models for range selectivity estimation. 将回归模型有效的使用在SE场景
In this work, we study whether regression techniques can be used for accurate selectivity estimation of multi-dimensional range predicates,
especially under the practical constraints of estimation time and memory footprint.
Our study includes neural networks and tree-based ensembles.
The choice of these techniques is governed by the following reasons:
(1) they have an inherent ability to learn complex, non-linear functions;
(2) recent work [9, 16, 24] has produced highly-optimized libraries based on these techniques.
Design choices for lightweight models. 对于轻量化模型的两点设计,对label取log;使用更多的启发式的SE作为扩展features
Notwithstanding(although) the promise, our initial exploration with these techniques resulted in inferior accuracy compared to simple baselines like AVI.
Although the learned models perform better as we increase the model size and complexity, we cannot afford arbitrarily large models.
We propose two simple, yet effective design choices that improve accuracy of models without increasing model size.
First, we use log-transformed version of regression labels.
While the transformation is very simple, it has a strong impact on the effectiveness of regression, particularly because relative error is more relevant in the selectivity estimation context [32].
Second, we use a set of heuristic selectivity estimators as extra features in addition to predicate ranges.
They help the model learn to differentiate between queries that have very similar range predicates but significantly different actual selectivities.
Importantly, these estimators are computationally effcient.
Both these design choices are generic and help both neural networks and tree-based ensembles.
Experimental evaluation highlights. 实验证明
We perform extensive empirical evaluation across multiple real-world datasets to show that the proposed models provide fast and highly accurate estimates for multi-dimensional ranges
compared to existing techniques including AVI, STHoles, uniform random sampling and a state-of-the-art kernel density based technique (KDE) [22] that improve over sampling.
......
BACKGROUND
(引出SE)When a declarative query is submitted to the database system, it is first optimized to identify a good (low latency) execution plan.
The quality of execution plan chosen by the query optimizer hugely depends on the quality of size estimates at intermediate stages of the plan, often termed as selectivity estimates.
Figure 3 gives an overview of how query processing architecture interacts with selectivity estimation module.

(描述SE过程)The selectivity estimation techniques usually have an off-line phase where they collect statistical information about database tables including row counts, domain bounds and histograms.
During query optimization, this information serves as the source for selectivity estimation techniques.
For example, consider a query with conjunction of multiple simple predicates (attribute - operator - constant) on different attributes of a database table.
Most database systems first compute selectivity fraction for each simple predicate using a histogram on the corresponding attribute.
Then, combined selectivity of conjunction is computed using an assumption regarding distribution of values across different attributes.
(多维SE,Combine的时候,两种假设)Below, we list two such assumptions:
1. Attribute Value Independence (AVI):
It assumes that values for different attributes were chosen independent of each other.
Under this assumption, the combined selectivity fraction for predicates on d attributes is calculated as

where sk is the selectivity fraction of predicate on kth attribute.
2. Exponential BackOff : 指数退避,仅考虑top4的fraction,并且combine的时候乘以指数
When attributes have correlated values, AVI assumption could cause signicant underestimations.
Microsoft SQL Server introduced an alternative assumption, termed as Exponential BackOff [3],
where combined selectivity fraction is calculated using only 4 most selective predicates with diminishing impact.
That is, combined selectivity is given by
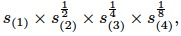
where s(k) represents kth most selective fraction across all predicates.
Opportunity.
The selectivities estimated using limited information available to estimation techniques can be hugely erroneous [27].
For instance, multi-dimensional range predicates on single table may suffer from estimation errors due to attribute correlations.
While modern database systems have support for limited multi-column statistics [7], the information is not suffcient to capture the correlation in fine granularity across numeric attributes.
While past research literature [14] has already noted that actual selectivities for predicates can be monitored with low overhead during query execution, and can be used to improve future estimates [15, 10, 40] - current systems do not fully exploit this opportunity.
Powerful regression methods are excellent candidates that can leverage the feedback information to learn good quality selectivity estimators.
当前的方法做SE的效果都很不尽人意,数据库本身也不具备给出列相关的相关统计。
之前的研究,已经指出在查询执行的时候,我们可以通过极小的overhead monitor到实际的SE,但是当前的研究没有很好的利用这样的数据
既然我们有历史的打标数据,本文认为回归模型是个不错的candidate来解决问题。
PROBLEM DESCRIPTION
Consider a table T with d numerical attributes A1,A2,......, Ad.
Let the domain for kth attribute be [mink, maxk].
Any conjunctive query q on numerical attributes of T can be represented in the following canonical form:

既然SE是个回归问题,那么首先要定义训练集,
首先任意query都可以表示成上面给出的这样的conjunction的predicate集合
这里需要注意的是,一个是需要补全,没有出现在查询中的predicate,相当于min <= a<= max;另外这种形式也适合于点查,即min=max
这样后面每个query都可以表示成一个等长的向量,完成形式化
同时作为训练集,需要label,这里的label就是act(query),相对于est(query)
在上面的形式化的前提下,回归问题就很容易描述了,如下
这里虽然没有对S中query分布做假设,但是有监督学习的限制,对于未学习到的多维区间很难给出精确的estimation,所以S set的构建对最终效果很关键
这里回归问题主要用于解决多维SE的问题,对于单列仍然使用histogram,对于单列histogram技术已经可以满足
Problem.
Given a set S of labeled queries, we wish to learn a regression model M, such that for any conjunctive range query q on T, M produces estimated selectivity est(q) close to the actual selectivity act(q).
Note that the problem definition does not make any assumption about the source and distribution of queries in the set S,
but the learned model M is expected to produce accurate estimates for queries that are well represented in the training set S.
Also, we highlight that our focus is on selectivity estimation for conjunction of two or more predicates, and we do not intend to replace single attribute histograms in the system metadata.
Formulation as a regression problem

Query Space.
To answer a query on a d-dimensional dataset, the regression model M takes as input a point location in the 2d-dimensional space defined over domain of range features - we call it query space.
The task for regression methods is to learn a function f over the query space to approximate the actual selectivity function.
Evaluation metrics
如何评价误差

CHOICE OF REGRESSION METHODS
(选择两种回归模型)To construct regression model M, we use non-linear regression techniques as the data can have non-linear, complex distributions in general.
We consider two types of generic non-linear regression methods: neural networks and tree-based ensembles.
Provided with suffcient training data, both methods can learn increasingly more complex regression functions with increase in the number of model parameters
and offer flexible accuracy-space tradeoff, as we describe in this section.
Background (介绍NN和tree-based,common sense)

Neural Network (NN).
We use the standard feed-forward neural network.
The simplest NN model has an input layer that consists of nodes to feed the vector of feature values as input and a single neuron output layer that produces the prediction value.
In addition to the neuron in the output layer, the network can have more neurons in the form of l hidden layers.
When l = 0, neural network is equivalent to a linear regression model. When l > 1, the network is referred to as a deep neural network.
We use neural network with fully connected layers, as visualized in Figure 4(a) for l = 2.
We use ReLU (Rectied Linear Unit) activations for neurons in the hidden layers.
The neuron in the output layer uses linear activation.
The total number of parameters in the model is a function of the number of input features and the number of neurons in each of the hidden layers.
Tree-based ensembles.
We consider both random forests and gradient boosted trees.
(bagging,每颗子树独立的训练和predicate,投票的方式决定最后结果,比较适用于分类,但是由于训练时的数据相同,很难独立,所以一般会把训练集进行放回采样,降低每颗子树之间的关联)
(boosting,每颗子树是为了降低前一个子树的错误率,一般针对前一个子树判断错的case进行加权训练,gradient意思是按倒数方向去优化模型,更适用于回归)
During training, the former uses bagging and the latter uses boosting as the ensemble strategy.
Both methods construct multiple binary trees. At the prediction time, each tree independently produces a prediction value using the input features.
To do this, each internal node in the tree uses exactly one input feature value to decide the next subtree, and each leaf node corresponds to a regression value.
The predictions from all the trees are aggregated to produce the final prediction of the ensemble.
Random forests use an unweighted average, and gradient boosted trees use a weighted sum to aggregate the predictions.
The model sizes for both are determined by the number of trees t and the number of leaves v in each tree.
Figure 4(b) shows an example tree-based ensemble model with t = 2 trees, each with v = 3 leaves where leaf nodes are shown as shaded circles.
MODEL DESIGN CHOICES
While larger size models can achieve ner granularity approximation, they also lead to increased estimation time.
This section discusses our model design choices to create compact models that can still capture complex functions.
Log-transformed labels
(对训练集的Label做以2为底的log,在estimation的时候再inverse转回来)
We generate training labels by applying log-transform (we use base 2) to selectivity value act(qi).
At estimation time, we apply inverse-transformation on model prediction to get the final estimation, i.e., est(qi) = 2p, where p is the model prediction.
While the transformation is very simple, it enables use of generic regression techniques for problem domains such as selectivity estimation, without
changing the implementation details of the technique - this is because selectivity
variation across different queries can be huge, and relative metric is more relevant, as explained next.
(这个design看着非常简单,作用主要是,可以更加focus在相对误差;capture abrupt selectivity variation in the query space with fewer parameters;详细参考原文)
Correlation based estimators as features
(增加额外的features可以大幅提升准确率,但是由于对于时空的限制,加feature需要同时满足effciency和relevance)
While both neural networks and tree-based models are capable of learning complex interactions between the basic input features,
using histograms and domain knowledge to manually engineer extra features can help improve selectivity estimation accuracy without increasing model size if the features are highly informative.
On the other hand, since we impose time and size constraint to the regression models, the additional features should satisfy the following basic criteria.
1. Effciency: Effcient derivation of feature values is important since it
causes additional overhead to estimation time for an ad hoc query (computing range features is already effcient).
2. Relevance: We require the added features to be highly relevant, i.e., strongly correlated with the actual selectivity.
Inclusion of irrelevant features may hurt as fewer model parameters would be available to capture the interaction among relevant features,
not to mention that it may cause unnecessary computations.
Heuristic estimators as features
(采用3种启发式的estimators当做扩充输入features)
The domain experts have designed simple heuristic estimators, e.g., AVI and EBO (described in Section 2)
that use information from single attribute histograms to produce selectivity estimates for conjunction of predicates.
In the same spirit as AVI, another estimator has been considered in the past [1], which returns the combined selectivity as the minimum selectivity across individual predicates - we call it the MinSel estimator.
We include the estimates based on all three heuristic estimators (AVI, EBO and MinSel) as extra input features to our regression models.
All of these estimators have a common first step, i.e., scanning the relevant histograms, followed by estimator specific simple computations.
The effciency is not a concern since single attribute histograms are typically independent of data size.
In our experiments, selectivity computation for each attribute took only 20-30 sec.
We justify relevance of these features in the remainder of this section.
Rationale: Varying degree of correlation
(3种estimators分别对应于从无关联,部分关联,完全关联,3种数据分布)
For a given conjunction of predicates, the combined actual selectivity depends on the degree of correlation among the individual predicates induced by the underlying data distribution.
The above set of estimators can capture various scenarios with different degrees of correlation, as explained next.
An estimator based on AVI assumption would produce good estimates if the predicates have no correlation between them.
MinSel estimator represents the other extreme compared to AVI, and produces good estimates when all predicates are satisfied by the same set of data rows, i.e., full correlation.
The EBO estimator is expected to capture some intermediate scenarios between complete independence and full correlation.
We observe that although each estimator is not accurate for all the queries, it may be accurate for a subset of queries and the model can learn the appropriate mapping from the training data.
We include these correlation based features (referred to as CE features) to demonstrate the impact of such features
that utilize information in single attribute histograms and we understand that including other estimators may also be helpful.
2d代表两个conjunction的predicate,对于不同的数据集,总有一个estimator远好于另外两个
We empirically validated the relevance of these features for different data distributions.
For each estimator, we found specific real-world datasets where it is signicantly better than the other two.
In Table 1, we show the percentage of queries with q-error <= 2 for different estimators across four datasets.
The first three workloads have 2-dimensional predicates on 3 different datasets (dataset1, dataset2 and dataset3).
We found that each estimator wins for one of the 2D datasets by a margin of at least 10%.

两个estimator结合后会产生互补,会大幅提升准确率
Our choice of these three estimators as features is further motivated by the observation that the CE features complement each other.
We demonstrate their complementary behavior using oracle combinations of individual estimators in Table 1.
Here, (AVI,EBO) corresponds to a hypothetical oracle that knows the better estimator between AVI and EBO to use for each individual query, and so on.
The oracle using all the three estimators has the best performance for all the datasets.
For example, it improves the percentage of queries with q-error <= 2 from 72% to 81% on dataset2.
(对于4d的数据集,无论是单个或combination的准确率都降低很多)
We emphasize using the 4D dataset in Table 1 that, while one of these estimators works reasonably well for 2D queries and they also complement each other well,
their accuracy for higher dimensional predicates is much worse than 2D queries.
For the 4D workload, the percentage of queries with q-error <= 2 lies in the range 12% to 50% for all three estimators as well as the hypothetical oracles.
(这些启发式的estimator虽然单独用回产生很大的误差,但用于学习模型的输入会有效的提升准确率,并且通过combination提升鲁棒性)
To summarize, choosing one of these estimators irrespective of(regardless of) data distribution clearly exposes database systems to the risk of large estimation errors for majority of queries.
However, using such estimators as input features to learned models provides a principled way to exploit their benefits and use model parameters to further improve accuracy.
In addition to improvement in accuracy, we empirically found that use of CE features also improve the robustness of the models against updates to the underlying datasets.
The intuition is that 1D histograms can be quickly updated to reflect the data distribution changes and model that uses CE features can use this updated information to improve estimates
with respect to the new actual selectivity, the details of the experiment can be found in Section 7.4
INTEGRATION WITH EXISTING DBMS
Regression models for multi-dimensional range selectivity estimation can be integrated into the existing system architecture as shown in Figure 5.
At a high level, the integration is conceptually similar to how it would be done for any generic multi-dimensional histograms, as both support estimation of conjunction of range predicates.
Below we discuss how these models are utilized by selectivity estimation module, followed by details on training of models.
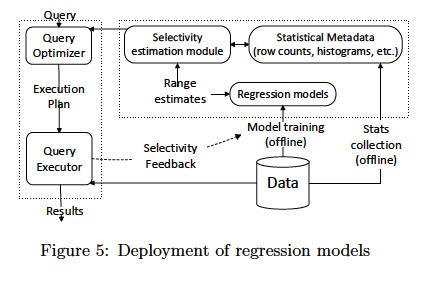
Estimation with regression models
Consider a model M1 trained for table T1 on attributes A1, A2, A3, A4 and another model M2 trained for T2 on attributes B5, B6, B7.
Model M1 can be used to estimate selectivity of conjunctive range predicates over any subset of the attributes A1 to A4,
by representing the predicate in canonical form defined in Section 3.
For example, M1 can produce estimate for A1 ^A2 or A2 ^A3 ^A4.
Similar argument holds for M2 regarding predicates on T2.
Given that pushing down base-predicates as filter operators on tables (before any join-operator) is a standard practice,
models M1 and M2 can serve any query that involve table T1, T2 or both.
If the query has additional predicates on same table, e.g. string predicates or predicates with IN clause,
existing methods in database systems or techniques from past work [30] can be used to combine partial information from different sources.
Overall, regression models help in fixing estimation errors due to correlations between range predicates at base-level of query plan trees where access path decisions are made.
Note that, fixing errors at the base of a plan tree would reduce the error propagated up the tree.
We have empirically evaluated models for up to moderately large (ten) number of attributes.
(当列很多的时候,是否需要用多个回归模型去学习)Table that have much larger number of numeric attributes, say 100, pose additional challenges for any technique including regression models.
It is unclear whether it is better to create a single model for all attributes or partition them to be handled by separate independent models [23].
It an interesting research problem beyond the scope of this paper.
Training regression models
Training a regression model requires a set of queries labeled with actual selectivities, and optionally CE feature values.
Feedback from past query executions is a natural source to collect such training data, at no explicit overhead.
In this respect, regression models resemble query-driven techniques proposed in the past [10, 12, 39, 22].
For any technique that takes only labeled queries as input, we can also think of a scenario
where we generate training examples to bootstrap the technique before receiving any external query.
Since collecting actual selectivities involves executing a large set of queries over the data,
it is quite resource consuming and takes up to (# rows # queries) operations since queries may have arbitrary overlap with each other.
There are several ways to reduce the latency.
First, we can use parallel resources, as the training process is offline.
Second, we can build an R-tree index on the query set, to reduce the number of queries to be checked for contain containment per data row.
Finally, we can also approximate actual selectivity labels by executing queries over a large enough sample of data and reduce latency by decreasing #rows per query.
We empirically study the resources needed for model training under this trade-o in Section 7.4.
(对于数据变化,是否需要重新训练,用CE features的时候对变化有一定适应性)
Impact of data updates. Models may need retraining whenever there is a significant shift in the query workload distribution or underlying data distribution, compared to initial training.
Such cases can be triggered by a bulk data update, similar to the triggers in existing engines [6] or a large fraction of served queries resulting in bad selectivity estimates compared to selectivities found after executions.
Once triggered, the new actual selectivity labels for existing training queries can be computed effciently if the system already supports a delta store for all updated rows in the data, which reduce # rows to be processed.
Otherwise, computing actual selectivities is identical to bootstrapping and similar ideas can be used to reduce overhead.
Interestingly, we found that models that use CE features do not necessarily need expensive retraining and can work reasonably well with updated 1D histograms.
We study the trade-offs available in case of database updates in Section 7.4.
RELATED WORK
Selectivity estimation in the context of query optimization has been an active area of research for multiple decades - we refer to [19] for an extensive survey.
Here, we provide a brief review of studies that are relevant to the goal of selectivity estimation for conjunctive range predicates.
Multi-dimensional histograms This is arguably(possibly) the most well studied approach to capture attribute correlations [35, 37].
The idea is to use multi-dimensional buckets that partition the data domain, to approximate the data distribution.
This approach faces challenges as dimensions increase because there are potentially many ways to identify buckets [19].
Also, the space requirement increases with the number of dimensions because the domain space increases exponentially and data can be skewed.
Later proposals [12, 21, 38] used overlapping buckets that allow a given number of buckets to identify more complex distributions,
they generally require more resources during bucket identication.
Query-driven histograms Query-driven (self-tuning) methods [10, 12, 39] are better designs in multi-dimensional histogram
as they focus only on regions in the subspaces that are being accessed by queries in the current workload.
The limitation of such methods is highlighted when workload is spread in large fraction of a high-dimensional space.
Sampling based methods Sampling based methods [42] have a lot of advantages as a data sample can represent any distribution without prior knowledge
and support a richer class of predicates beyond range predicates.
Their key weaknesses are (a) low accuracy for highly selective predicates and (b) high estimation cost because calculating an estimate requires a full scan over the samples [22].
Kernel density estimators(KDE) [21, 22] can provide signicantly improved accuracy for given sample size.
But such techniques [22] are designed for futuristic(未来派) platforms when GPUs are common-place.
Also, they do not avoid scanning a large sample at estimation time, which is slow without parallel resources.
There have been recent proposals [34, 25] that combine information from both histograms and samples to handle the issue of highly selective predicates,
but they do not meet the practical requirements of small memory footprint and estimation time.
Learned models Use of machine learning techniques for selectivity estimation is not new, prior work explored different models
ranging from curve-fitting[15], wavelets [31], to probabilistic graphical models [20, 41].
Infact some early works also use neural network based models for selectivity estimation over small number of attribute [11, 26, 29, 28].
Despite these attempts, fast and accurate selectivity estimation for multi-dimensional range predicates was a blindspot.
In this paper, we demonstrate signicant progress on this important problem with extensive evaluation on multiple real-world datasets.
Most recently, [25] targeted correlations across joins using a custom neural network architecture.
While [25] certainly addresses generic version of the selectivity estimation problem, the models in this paper are much more succinct(简洁的) leading to signicantly faster estimations.
Also, we do not confine(limit) the regression techniques to be neural network, and found that tree-based ensembles are much faster to train compared to neural networks.
CONCLUSION AND FUTURE WORK
This paper explored the application of standard regression techniques to selectivity estimation of range predicates.
We showed that lightweight models can be designed to to deliver fast and accurate estimates for multi-dimensional range predicates.
With extensive (widely) empirical evaluation over multiple real world datasets,
we found that the accuracy of models is signicantly better than existing methods in database systems, with reasonably small training eort.
We believe that the learned models can add signicant value to existing systems, due to desirable properties such as small memory footprint and simple estimate routines.
There are several interesting directions for future work including automatically deciding the attribute subsets for model construction;
handling larger class of queries such as join queries with arbitrary filters etc.
We see this work as an initial step towards using learning techniques to improve the state of selectivity estimation under practical constraint of small query optimization time.
