二维偏序问题,用树状数组解决。
本题看似二维,但给出的数据就是已经按照y从小到大排好序的,也就是说,当前读到一个点的时候,当前点的y坐标肯定比已经读入的大,或者等于。就算是等于的话,也是x坐标比我当前点的x坐标小。这样一来,我们如果按照读入顺序来处理,则保证了后面点的y坐标一定大于前面的点,所以我们每次只需统计x坐标比我们当前点小的个数就行了。
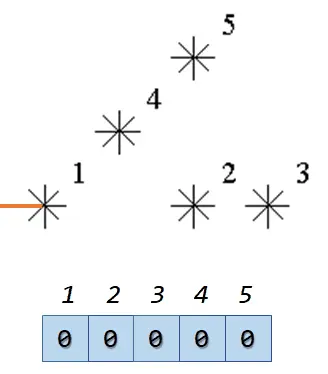
注意:给的点的坐标是从0开始的,树状数组下标从1开始(0的位置不可用),所以需要在输入x坐标时+1处理。
const int N=15010,M=32010;
PII a[N];
int c[M];
int cnt[N];
int n;
int lowbit(int x)
{
return x&-x;
}
void add(int x,int v)
{
for(int i=x;i<M;i+=lowbit(i))
c[i]+=v;
}
int sum(int x)
{
int res=0;
for(int i=x;i;i-=lowbit(i))
res+=c[i];
return res;
}
int main()
{
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i].fi>>a[i].se;
a[i].fi++;
cnt[sum(a[i].fi)]++;
add(a[i].fi,1);
}
for(int i=0;i<n;i++) cout<<cnt[i]<<endl;
//system("pause");
return 0;
}