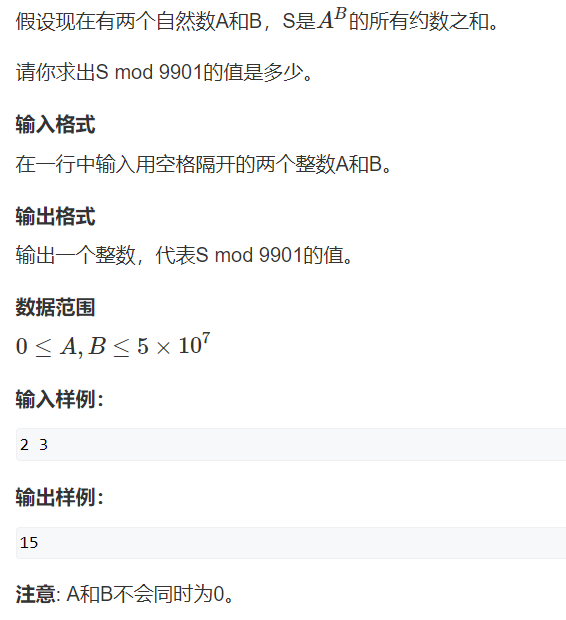
分治:分治法把一个问题划分为若干个规模更小的同类子问题,对这些子问题递归求解,然后
在回溯时通过它们推导出原问题的解
首先把A分解质因数:A = p1 ^ k1 * p2 ^ k2 * ... * pn ^ kn
然后A一共的约数个数是:
(k1 + 1) * (k2 + 1) * ... * (kn + 1)
然后A的所有约数之和是:
(p1^0 + p1^1 + ... + p1^k1) * (p2^0 + p2^1 + ... + p2^k2) * ... * (pn^0 + pn^1 + ... + pn^kn)
可以用分治的思想来求sum(p, k) = p^0 + p^1 + ... + p^k
然后A ^ B = p1 ^ k1B * p2 ^ k2B * ... * pn ^ knB
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int mod = 9901; 4 int qmi(int a, int k) { 5 a %= mod; 6 int res = 1; 7 while (k) { 8 if (k & 1) { 9 res = res * a % mod; 10 } 11 a = a * a % mod; 12 k >>= 1; 13 } 14 return res; 15 } 16 int sum(int p, int k) { //求p^0 + p^1 + ... + p^k的和 17 if (k == 0) { 18 return 1; 19 } 20 if ((k & 1) == 0) { //如果k是偶数 21 return (p % mod * sum(p, k - 1) + 1) % mod; 22 //return ((1 + qmi(p, k / 2)) % mod * sum(p, k / 2 - 1)) % mod + qmi(p, k) % mod; 23 } 24 //如果k是奇数 25 return (1 + qmi(p, (k + 1) / 2)) * sum(p, (k - 1) / 2) % mod; 26 } 27 int main() { 28 int A, B; 29 cin >> A >> B; 30 if (A == 0) { //特判 31 cout << 0 << endl; 32 return 0; 33 } 34 int res = 1; 35 for (int i = 2; i <= A; i++) { //对A分解质因数 36 int s = 0; 37 while (A % i == 0) { 38 s++; 39 A /= i; 40 } 41 if (s) { 42 res = res * sum(i, s * B) % mod; 43 } 44 } 45 cout << res << endl; 46 return 0; 47 }