

卢卡斯定理lucas


然后就可以根据这个公式来求组合数了
时间复杂度:O(log p (n) * p log 2 (p)) 。其中的log p (n)是计算a%mod和b%mod所要的时间
然后化简
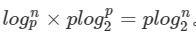
最终时间复杂度可以记为:O(p * log 2 (n)),n是是C(n,m)的下界n,p是取模用的质数
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 int p; 5 ll qmi(ll a, ll b) { 6 ll res = 1; 7 while (b) { 8 if (b & 1) { 9 res = res * a % p; 10 } 11 a = a * a % p; 12 b >>= 1; 13 } 14 return res; 15 } 16 ll C(ll a, ll b) { //用定义直接用逆元求 17 ll res = 1; 18 for (int i = 1, j = a; i <= b; i++, j--) { 19 res = res * j % p; 20 res = res * qmi(i, p - 2) % p; 21 } 22 return res; 23 } 24 ll lucas(ll a, ll b) { 25 if (a < p && b < p) { 26 return C(a, b); //从定义来算 27 } 28 return C(a % p, b % p) * lucas(a / p, b / p) % p; //用卢卡斯定理来算 29 } 30 int main() { 31 int n; 32 cin >> n; 33 while (n--) { 34 ll a, b; 35 cin >> a >> b >> p; 36 cout << lucas(a, b) << endl; 37 } 38 return 0; 39 }