

预备知识:裴蜀定理

a和b的最大公约数就是a和b能凑出来的最小的正整数
扩展欧几里得算法就是构造出来一种方式,使得对于任意的整数a和b,一定存在整数x和y,满足上式
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 ll exgcd(ll a, ll b, ll &x, ll &y) { 5 if (!b) { 6 x = 1; 7 y = 0; 8 //x = 1, y = 0是一组解 9 return a; 10 } 11 ll d = exgcd(b, a % b, y, x); //翻转一下 12 /* 13 当上一行的递归结束时 14 一定有b * y + (a % b) * x = (a, b) = d成立 15 然后把上面的式子拆开,看看a和b的系数是什么 16 首先 a mod b = a - floor(a / b) * b; 17 计算过程见下图 18 */ 19 y -= a / b * x; 20 return d; 21 } 22 int main() { 23 ios::sync_with_stdio(false); 24 cin.tie(0); 25 cout.tie(0); 26 int n; 27 cin >> n; 28 while (n--) { 29 ll a, b, x, y; 30 cin >> a >> b; 31 exgcd(a, b, x, y); 32 cout << x << " " << y << endl; 33 } 34 return 0; 35 }
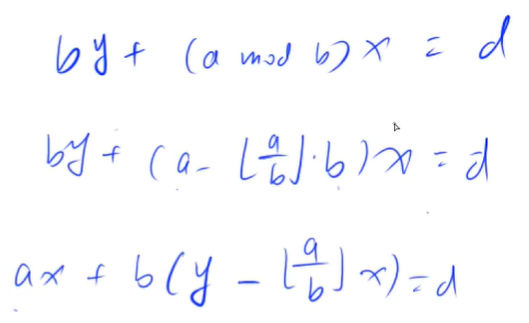
解不唯一,只要求出一组解,就可以求出其通解
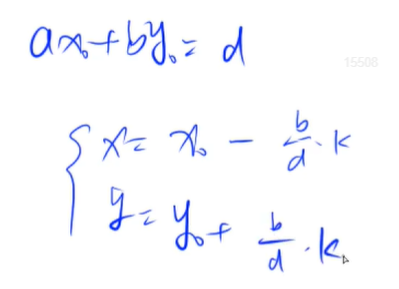
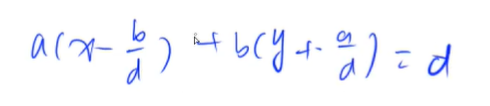
k是整数,参考资料:https://www.acwing.com/solution/content/1393/