


哈希表的时间复杂度近似O(1)
什么情况下需要用到哈希表
把一个庞大的值域,映射到一个较小的(10 ^ 5 ~ 10 ^ 6左右)值域

之前的离散化是一种极其特殊的哈希方式,之前的离散化需要保序的,需要保证单调递增
现在说的是一般意义的哈希
定义一个哈希函数h()
使得h(x)的值域属于0 ~ 10 ^ 5, x的取值范围是 -10 ^ 9 ~ 10 ^ 9
一般情况下,哈希函数可以直接取模
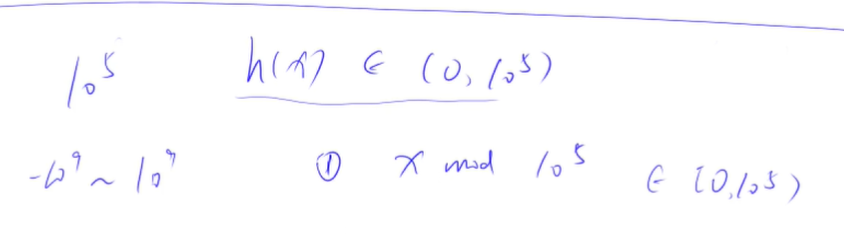
然后还需要处理一下冲突的问题
如果两个不同的数经过哈希函数之后,映射成了相同的一个数如何解决
按照处理冲突的方式,把哈希表分为两种,开放寻址法和拉链法
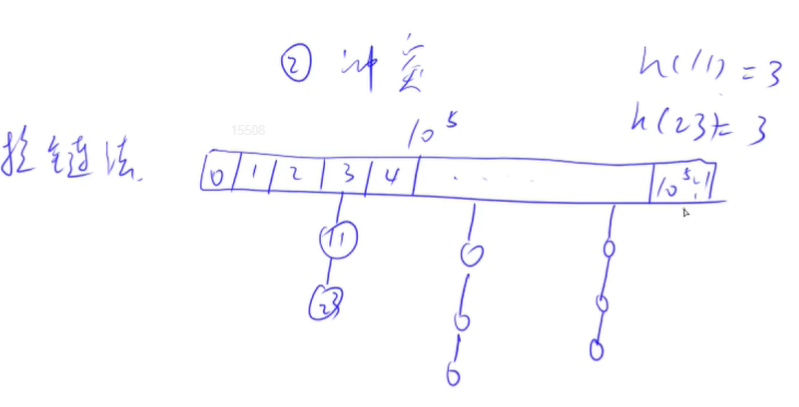
拉链法:
图论里面存点的时候,用到的存储结构和拉链法相同
首先开个一维数组,来存储所有的哈希值
每一个槽上拉一条链(单链表),来存储这个槽上当前有的所有数
一般情况下,算法题目不需要在哈希表中删除元素。一般只有添加和查找两个操作
如果真要删除,不是真正的把这个元素从表中删除。可以再开一个数组,打一个标记,表示这个点被删除了
拉链法代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 //拉链法 4 const int N = 100003; 5 //取模的时候要取质数,而且要离2的整次幂尽可能远 6 //这样冲突的概率最小 7 int h[N], e[N], ne[N], idx; 8 //h数组是槽,其余和单链表一样 9 void insert(int x) { //插入操作 10 int k = (x % N + N) % N; 11 //k是哈希值 12 e[idx] = x; 13 ne[idx] = h[k]; //头插法 14 h[k] = idx; 15 idx++; 16 } 17 bool find(int x) { //查询操作 18 int k = (x % N + N) % N; 19 for (int i = h[k]; i != -1; i = ne[i]) { 20 if (e[i] == x) { 21 return true; 22 } 23 } 24 return false; 25 } 26 int main() { 27 memset(h, -1, sizeof(h)); //把所有槽清空,单链表的空指针用-1表示 28 int n; 29 cin >> n; 30 while (n--) { 31 string op; 32 int x; 33 cin >> op; 34 if (op == "I") { 35 cin >> x; 36 insert(x); 37 } else { 38 cin >> x; 39 if (find(x)) { //如果能找到x这个数的话 40 cout << "Yes" << endl; 41 } else { 42 cout << "No" << endl; 43 } 44 } 45 } 46 return 0; 47 }
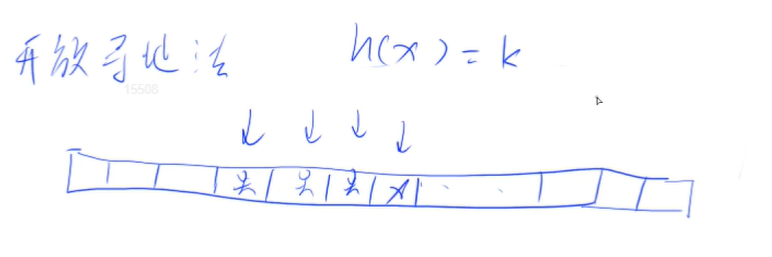
开放寻址法:
只开一维数组
这个一维数组的长度,经验上看,要开到题目数据范围的2 ~ 3倍
开放寻址法处理冲突的思路是:冲突了就往后找,直到空了
开放寻址法代码
1 #include <bits/stdc++.h> 2 using namespace std; 3 const int N = 200003, null = 0x3f3f3f3f; 4 //如果数组上的数是null的话,表示这个位置上是空 5 //这个数只要不在题目的数据范围内就好了 6 int h[N]; 7 int find(int x) { 8 //如果x在哈希表中已经存在的话,返回x所在的位置 9 //如果x在哈希表中不存在的话,返回x应该存储的位置 10 int k = (x % N + N) % N; 11 while (h[k] != null && h[k] != x) { 12 k++; 13 if (k == N) { 14 k = 0; 15 } 16 } 17 return k; 18 } 19 int main() { 20 memset(h, 0x3f, sizeof(h)); 21 int n; 22 cin >> n; 23 while (n--) { 24 string op; 25 int x; 26 cin >> op >> x; 27 if (op == "I") { 28 int k = find(x); 29 h[k] = x; 30 } else { 31 int k = find(x); 32 if (h[k] != null) { 33 cout << "Yes" << endl; 34 } else { 35 cout << "No" << endl; 36 } 37 } 38 } 39 return 0; 40 }