14.模拟堆

 

主要用在图论的Dijkstra算法

首先需要知道第k个插入的点是堆里面的哪个点

还需要知道堆里面的某个点是第几个插入的点

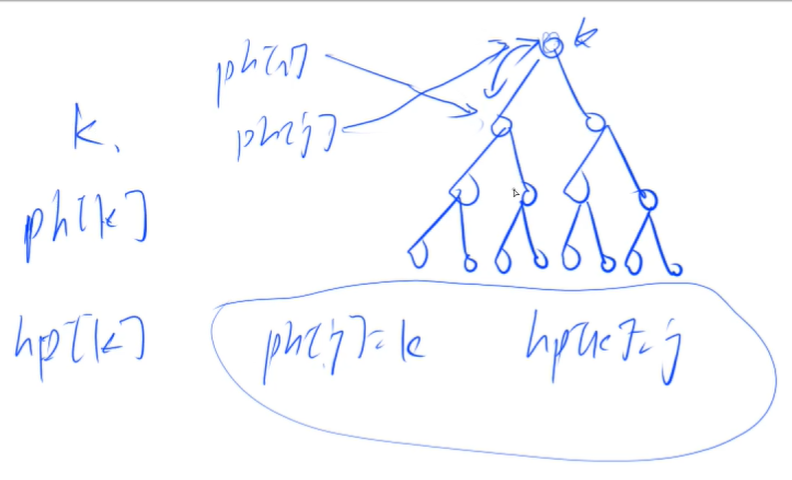
 第j个插入的点是堆里面的k

堆里面的k是第j个插入的点

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
int h[N], se;
int ph[N], hp[N];
//ph[k]存储第k个插入的数在堆里的下标
//hp[k]堆里面的点是第几个插入的点 
void heap_swap(int a, int b) {
    swap(ph[hp[a]], ph[hp[b]]);
    swap(hp[a], hp[b]); 
    swap(h[a], h[b]); //交换两个值
} 
void down(int u) {
    int t = u;
    if (u * 2 <= se && h[u * 2] < h[t]) {
        t = u * 2;
    }
    if (u * 2 + 1 <= se && h[u * 2 + 1] < h[t]) {
        t = u * 2 + 1;
    }
    if (u != t) {
        heap_swap(u, t);
        down(t);
    }
}
void up(int u) {
    while (u / 2 && h[u / 2] > h[u]) {
        heap_swap(u / 2, u);
        u /= 2;
    }
}
int main() {
    int n;
    cin >> n;
    int m = 0; //表示是当前第几个插入的数
    while (n--) {
        string s;
        int k, x;
        cin >> s;
        if (s == "I") {
            cin >> x;
            se++;
            m++;
            ph[m] = se; //插入新的数，放在末尾
            hp[se] = m;
            h[se] = x;
            up(se);
        } else if (s == "PM") {
            cout << h[1] << endl;
        } else if (s == "DM") {
            heap_swap(1, se);
            se--;
            down(1);
        } else if (s == "D") {
            cin >> k;
            k = ph[k]; //让k等于第k个插入的数在堆里面的位置
            heap_swap(k, se);
            se--;
            down(k);
            up(k);
        } else {
            cin >> k >> x;
            k = ph[k];
            h[k] = x;
            down(k);
            up(k);
        }
    }
    return 0;
}