
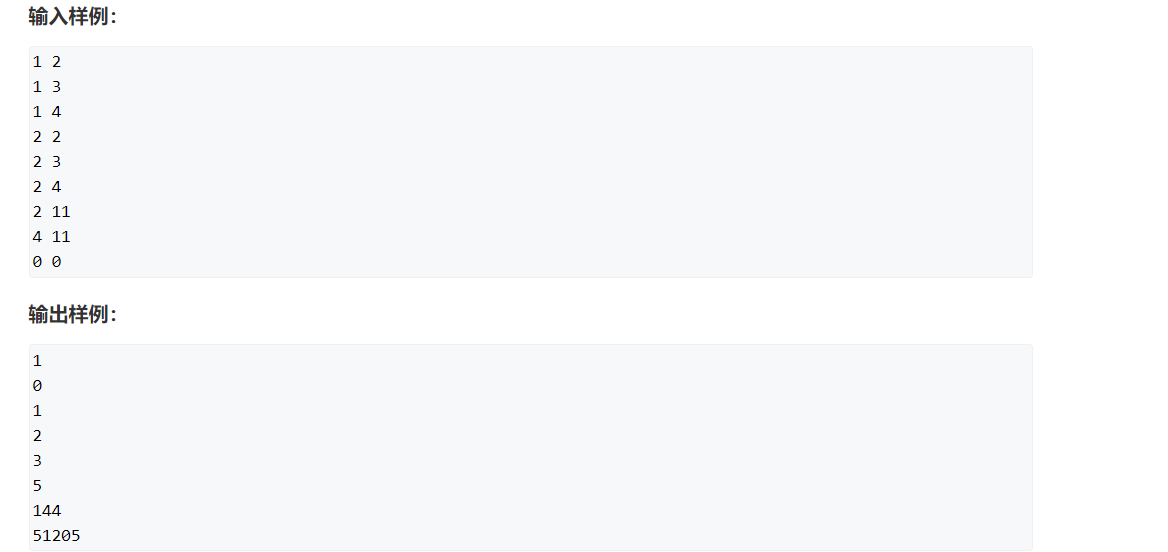
位运算 + 二进制表示状态 = 状态压缩DP
先把横着的小方块放好,然后剩下位置用竖着的小方块填充
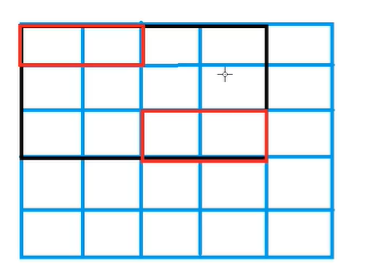
然后就转化为求横着摆放小方块的方案数
按列来求
状态表示:
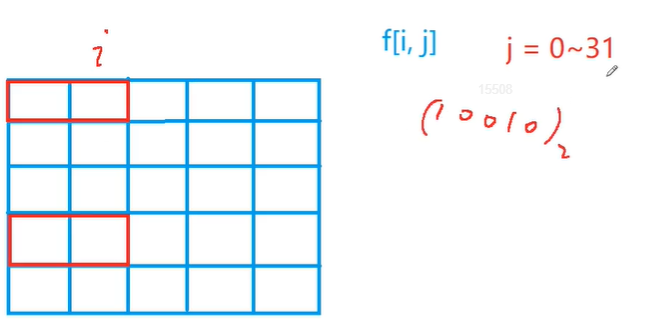
dp[i][j]表示所有摆到了第i列,然后上一列伸出来的小方块的状态是j的情况下,总的方案数
状态转移:
枚举一下i - 1列的状态
比如说当前状态是j = 00001
然后上一个状态i - 1是k = 10010
从i - 1列伸到第i列的:j = 00001
从i - 2列伸到第i - 1列的:k = 10010
位运算的预备知识
与运算 &
或运算 |

条件一:不能有冲突。
也就是需要判断(j & k)== 0,若等于0,表示没有冲突
条件二:第i - 1列空余格子一定是连续的,且是偶数,因为要竖着放小方块
j | k里面,所有0的位置,就是第i - 1列所有空白的格子
就是j | k里面不能存在连续奇数个0
只要满足这两个条件,就可以转移过来
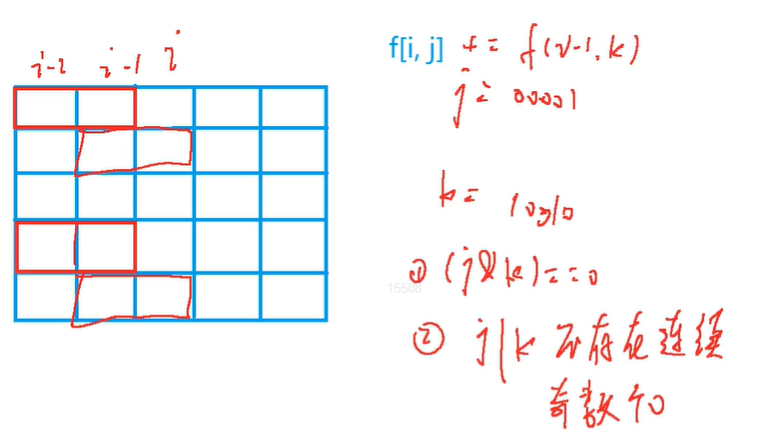
把所有满足条件的k加起来,就是状态转移方程
状态数量:11 * 2 ^ 11
转移数量:2 ^ 11
时间复杂度: 11 * 2 ^ 11 * 2 ^ 11 = 4 * 10 ^ 7
2020年7月31日复习更新:关于dp[0][0]为什么初始化为1
在下面代码31行,求dp数组的过程时,是从第1列开始枚举的,但是之后需要用到dp[i - 1][]
从dp数组的定义入手考虑,dp[i][j]表示所有摆到了第i列,然后上一列伸出来的小方块的状态是j的情况下,总的方案数
i的含义是这是第i列
j的含义是从第i - 1列伸出来的小方块的状态是j
当i = 0时,i - 1 = -1,第-1列不会有小方块,所以第i列的状态一定是0
dp[0][0] = 1表示不放也是一种方案,这是dp问题统计方案数的重点

1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int N = 13, M = 1 << N; 5 ll dp[N][M]; 6 bool st[M]; 7 int main() { 8 int n, m; 9 while (cin >> n >> m && n != 0) { 10 //预处理一下,所有的状态是否不存在连续奇数个0 11 for (int i = 0; i < (1 << n); i++) { //遍历所有的状态 12 st[i] = true; //假设是成立的 13 int cnt = 0; //cnt是当前这一段连续0的个数 14 for (int j = 0; j < n; j++) { //n是这个二进制数的位数 15 if (i >> j & 1) { //如果当前这一位是1,说明上一段已经截止了 16 if (cnt & 1) { //判断上一段连续的0是否是奇数个,若是 17 st[i] = false; //说明第i个状态时不合法的,存在了连续奇数个0 18 } 19 cnt = 0; //遇到1以后,连续奇数个0已经结束了,新开始一段 20 } else { 21 cnt++; 22 } 23 } 24 if (cnt & 1) { //然后判断最后一段0的个数 25 st[i] = false; 26 } 27 } 28 //然后是dp的过程 29 memset(dp, 0, sizeof dp); //把dp数组置为0 30 dp[0][0] = 1; //边界情况 31 for (int i = 1; i <= m; i++) { //枚举所有的列 32 for (int j = 0; j < (1 << n); j++) { //枚举第i列的所有状态 33 for (int k = 0; k < (1 << n); k++) { //再枚举第i - 1列的所有状态 34 if ((j & k) == 0 && st[j | k]) { 35 dp[i][j] += dp[i - 1][k]; 36 } 37 } 38 } 39 } 40 cout << dp[m][0] << endl; //答案 41 } 42 return 0; 43 }