2019软件工程第三次作业---付志峰

（一）题目要求：

问题： 给定n个整数（可能为负数）组成的序列a[1],a[2],a[3],…,a[n],求该序列如a[i]+a[i+1]+…+a[j]的子段和的最大值。当所给的整数均为负数时定义子段和为0，依此定义，所求的最优值为： Max{0,a[i]+a[i+1]+…+a[j]},1<=i<=j<=n
例如，当（a[1],a[2],a[3],a[4],a[5],a[6]）=(-2,11,-4,13,-5,-2)时，最大子段和为20。
-- 引用自《百度百科》

（二）源代码：

https://git.dev.tencent.com/dtid_c73f155b556a874e/fzf.git

#include<stdio.h>

int Max(int a[], int n)  
{  
	int sum, Max;  
	sum = Max = 0;  
	int i, j;  
	for (i = 0; i < n; i++)  
	{  
		sum = 0;  
		for (j = i; j < n; j++)  
		{  
			sum += a[j];  
			if (sum > Max)  
				Max= sum;  
		}  
	}  
	return Max;  
}  

int main()
{
	int a[100],num;
	scanf_s("%d",&num);
	for (int i = 0; i <num; i++)
	{
		scanf_s("%d",&a[i]);
	}
	printf("%d", Max(a, num));
	return 0;
}

（三）流程图：

（四）单元测试代码：

判定覆盖
由流程图可知，需要测试以下数据
thissum>sum
thissum<=sum
thissum>0
thissum<=0
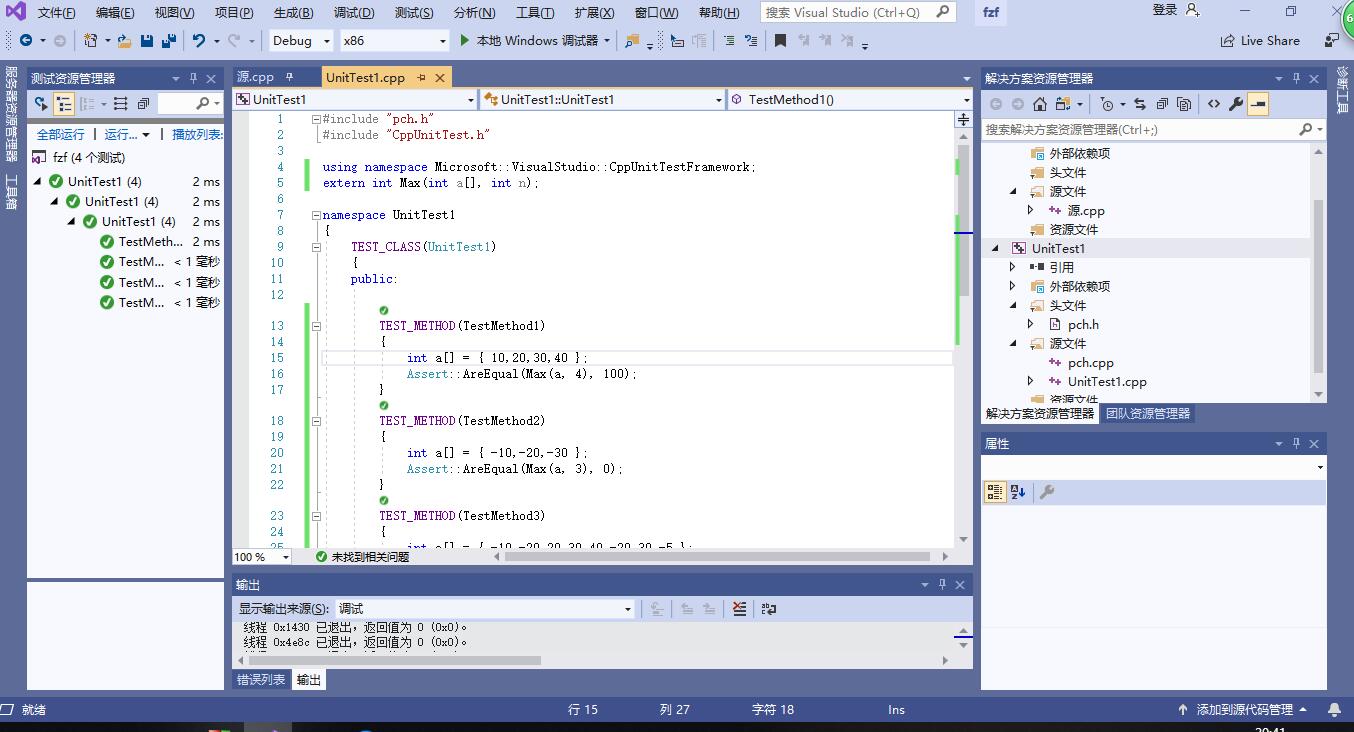
使用单元测试代码测试程序，具体代码如下：

#include "pch.h"
#include "CppUnitTest.h"

using namespace Microsoft::VisualStudio::CppUnitTestFramework;
extern int Max(int a[], int n);

namespace UnitTest1
{
	TEST_CLASS(UnitTest1)
	{
	public:
		
		TEST_METHOD(TestMethod1)
		{
			int a[] = { 10,20,30,40 };
			Assert::AreEqual(Max(a, 4), 100);
		}
		TEST_METHOD(TestMethod2)
		{
			int a[] = { -10,-20,-30 };
			Assert::AreEqual(Max(a, 3), 0);
		}
		TEST_METHOD(TestMethod3)
		{
			int a[] = { -10,-20,20,30,40,-20,30,-5 };
			Assert::AreEqual(Max(a, 8), 100);
		}
		TEST_METHOD(TestMethod4)
		{
			int* a = 0;
			Assert::AreEqual(Max(a, 0), 0);
		}
	};
}

（五）测试结果：