之前分为两部分讨论过SVM。第一部分讨论了线性SVM,并且针对线性不可分的数据,把原始的问题转化为对偶的SVM求解。http://www.cnblogs.com/futurehau/p/6143178.html
然后考虑到特征数量特别特别多的时候,引入核函数的求解。http://www.cnblogs.com/futurehau/p/6149558.html
但是,之前也遗留了一个问题,就是比如高斯核函数或其他的核函数,虽然large margin能够在一定程度上防止过拟合,但是加入你的核函数太过于powerful的话,还是很有可能带来overfit的问题。另一方面,之前都是基于hard Margin,就是要求你所有的数据都给我分正确,这很容易带来过拟合的问题。
所以,接下来就讨论soft margin来避免过拟合问题。简单来说soft margin就是允许模型犯一些的错误。
一、soft margin 的引入
如下图所示,我们把原来的hard margin转化为soft margin,允许你在一些点处犯错误,但是最小化的式子就需要改变,意思是你错误的点要尽可能的少。c是用来权衡soft margin和容许犯的错误大小的超参数。

稍微转化一下,表达式变为:

但是我们发现,这样一个表达式并不是一个QP问题的,因为取0取1这个的引入导致是非线性的,那么我们应该怎么转化呢?
这样思考,之前我们只考虑了分正确没,对于不正确的都一视同仁。我们可不可以改变一下呢?对于那些不正确的,如果离边界比较远的其实是大错误,如果离边界比较近的其实是小错误,这两类错误其实是应该区分开来的,所以引入新的表达式如下:

使用伊布c龙来记录违反的大小。表明你离我想要的值到底有多远。
这样,我们的问题就转化为:

观察这个表达式,其实也可以看为给定松弛因子做目标函数,给定一个L2的正则项。

二、soft margin 的 dual problem
好了,我们之前得到原始的soft margin 问题:

类似于之前的方法,我们需要把这个问题转换为对偶问题。
写出拉格朗日函数:

目标:

对伊布c隆求导得到:

带回原来表达式化简得到:

得到最终的表达式:

我们发现,最终的soft Margin dual problem的表达式和hard margin的表达式是内部是一样的,区别在于alpha的范围变化了。所以类似于之前的内部求偏导,我们可以得到:

对比之前,唯一的区别就是alpha的范围改变了。
三、参数b的计算与图形分析
3.1 b的求解
之前得到了几个参数,还差b。b的表达和之前有所不同,这里特别分析。

只有第二个等式C不等于alpha的时候才有确定的解,否则只能由kkt条件给出一个范围。

3.2 C的影响

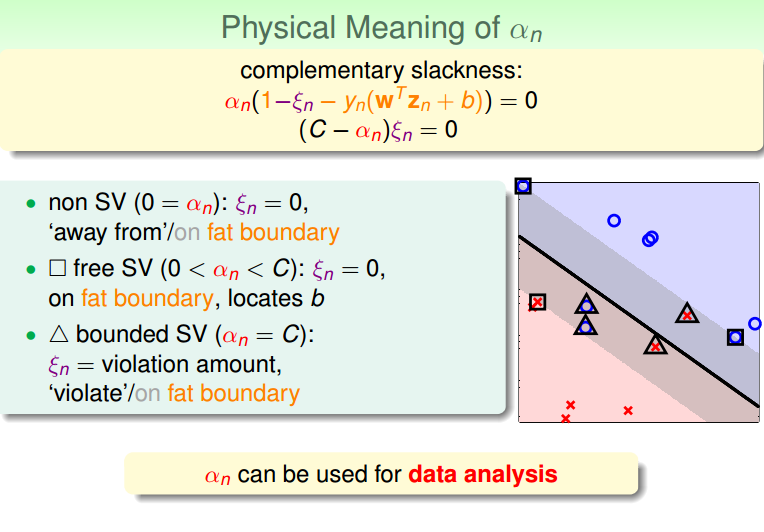
3.3 alpha的物理意义


4. leave one out cross validation
还不太理解。