CF414D Mashmokh and Water Tanks

CF414D Mashmokh and Water Tanks

洛谷评测传送门

题目描述

Mashmokh is playing a new game. In the beginning he has kk liters of water and pp coins. Additionally he has a rooted tree (an undirected connected acyclic graph) that consists of mm vertices. Each vertex of the tree contains a water tank that is empty in the beginning.

The game begins with the fact that Mashmokh chooses some (no more than kk ) of these tanks (except the root) and pours into each of them exactly 11 liter of water. Then the following process is performed until there is no water remained in tanks.

• The process consists of several steps.
• At the beginning of each step Mashmokh opens doors of all tanks. Then Mashmokh closes doors of some tanks (he is not allowed to close door of tank in the root) for the duration of this move. Let's denote the number of liters in some tank with closed door as ww , Mashmokh pays ww coins for the closing of that tank during this move.
• Let's denote by x_{1},x_{2},...,x_{m}x1,x2,...,x**m as the list of vertices of the tree sorted (nondecreasing) by their depth. The vertices from this list should be considered one by one in the order. Firstly vertex x_{1}x1 (which is the root itself) is emptied. Then for each vertex x_{i}x**i (i>1) , if its door is closed then skip the vertex else move all the water from the tank of vertex x_{i}x**i to the tank of its father (even if the tank of the father is closed).

Suppose ll moves were made until the tree became empty. Let's denote the amount of water inside the tank of the root after the ii -th move by w_{i}w**i then Mashmokh will win max(w_{1},w_{2},...,w_{l})max(w1,w2,...,w**l) dollars. Mashmokh wanted to know what is the maximum amount of dollars he can win by playing the above game. He asked you to find this value for him.

输入格式

The first line of the input contains three space-separated integers m,k,p (2<=m<=10^{5}; 0<=k,p<=10^{9})m,k,p (2<=m<=105; 0<=k,p<=109) .

Each of the following m-1m−1 lines contains two space-separated integers a_{i},b_{i} (1<=a_{i},b_{i}<=m; a_{i}≠b_{i})a**i,b**i (1<=a**i,b**i<=m; a**i�=b**i) — the edges of the tree.

Consider that the vertices of the tree are numbered from 1 to mm . The root of the tree has number 1.

输出格式

Output a single integer, the number Mashmokh asked you to find.

题意翻译

给你一棵树，k升水，p块钱，进行一次游戏。 在游戏进行前，可以在任意个节点上放置1升水（总数不超过k）
游戏进行若干轮，每轮游戏开放所有节点，可以选择若干个节点关闭，代价为该节点的水数量。然后所有未关闭的节点的水流向它的父亲(不会连续移动)。

最后，根节点中的水会被取走，水的数量为该轮游戏的盈利。
求盈利最大的某轮游戏的盈利。

输入输出样例

输入 #1复制

输出 #1复制

输入 #2复制

输出 #2复制

说明/提示

The tree in the first sample is shown on the picture below. The black, red, blue colors correspond to vertices with 0, 1, 2 liters of water.

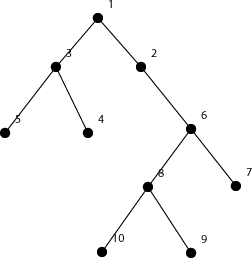One way to achieve the maximum amount of money is to put 1 liter of water in each of vertices 3 and 4. The beginning state is shown on the picture below.

Then in the first move Mashmokh will pay one token to close the door of the third vertex tank. The tree after the first move is shown on the picture below.

After the second move there are 2 liters of water in the root as shown on the picture below.

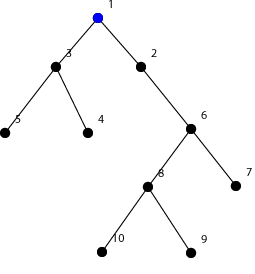
题解：

2019.11.13模拟赛T3 40分场

在此吹爆同届大佬@iamrjj，考场爆切黑题，简直是中国OI的先驱，IOI的未来！

（由于和我们考试的题面不一样，我简单概括一下题意：）

题目大意

给一棵树，一开始(k)个人可以被放在树上除根节点之外的节点，但是每个节点只能放(1)个人。每一秒钟你可以往一些地方放路障拦住这里的所有人，花费的价值为当前点的人数。如果这个时刻这个点没有路障，这个点的所有人会向上爬一个点，这样的话，一些时刻会有人抵达根节点，现在需要你分配放路障的地方和时间，求所有时刻最多的抵达根节点的人数是多少。

题解：

在考场上连暴力都不会写。所以我仔细观察了一下样例，我发现，如果通过技术手段把人都拦在根节点的儿子节点上，直到所有人都到达根节点的儿子节点们，这个时候同时放开拦截，这些人就会同时抵达终点。这种方法就是最优秀的（刨除其他的一切条件）

所以我就乱搞（骗分），如果(k<n)，输出(k)，否则输出(n-1)。成功40分。

正经题解：

这回考虑其他的因素，我们发现最优的决策一定是越来越多的人都在到达根节点之前到达同一深度，同理，那么两个人一开始被放置的位置深度差越大，把一个人拦下使得另一个人追上他的难度（花费）就越大。所以我们要尽可能地让人们的初始深度差值最小。也就是说，我们要将其放在：按深度排序后深度相邻的点上。

那么我们把这些点按深度排序为(l-r)。假设深度为(depth)的点上有(cnt[depth])个放上人。所有放人的节点中深度最大的为(D)。那么为了让他们达到统一深度，需要付出的钱是：

[sum_{i=l}^{i=r}{(D-deep[i])} ]

那么当(r)变大的时候代价也变大。(l)变大的时候代价会变小。为了控制这个(l-r)的范围，我们当然选用双指针法（尺取法）

关于尺取法和双指针，如有不太会的同学可以翻看蒟蒻的这篇博客：

尺取法详解

AC代码：

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1e5+10;
int n,k,p;
int tot,head[maxn],nxt[maxn<<1],to[maxn<<1];
int deep[maxn],cnt[maxn];
void add(int x,int y)
{
	to[++tot]=y;
	nxt[tot]=head[x];
	head[x]=tot;
}
void dfs(int x,int f)
{
	deep[x]=deep[f]+1;
	cnt[deep[x]]++;
	for(int i=head[x];i;i=nxt[i])
	{
		int y=to[i];
		if(y==f)
			continue;
		dfs(y,x);
	}
}
int main()
{
	scanf("%d%d%d",&n,&k,&p);
	for(int i=1;i<n;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		add(x,y);
		add(y,x);
	}
	dfs(1,0);
	sort(deep+1,deep+n+1);
	int l=2,r=2,ans=1,tmp=0;
	while(1)
	{
		if(l>=n || r>=n)
			break;
		r++;
		if(deep[r]!=deep[r-1])
			tmp+=(r-l);
		while(tmp>p || r-l+1>k)
		{
			tmp-=(deep[r]-deep[l]);
			l++;
		}
		ans=max(ans,(r-l+1));
	}
	printf("%d",ans);
	return 0;
}