洛谷 P1941 飞扬的小鸟
JDOJ 2887: [NOIP2014]飞扬的小鸟 D1 T3
Description
Flappy Bird 是一款风靡一时的休闲手机游戏。玩家需要不断控制点击手机屏幕的频率来调节小鸟的飞行高度,让小鸟顺利通过画面右方的管道缝隙。如果小鸟一不小心撞到了水管或者掉在地上的话,便宣告失败。
为了简化问题,我们对游戏规则进行了简化和改编:
- 游戏界面是一个长为 n,高为 m的二维平面,其中有 k个管道(忽略管道的宽度)。
- 小鸟始终在游戏界面内移动。小鸟从游戏界面最左边任意整数高度位置出发,到达游戏界面最右边时,游戏完成。
- 小鸟每个单位时间沿横坐标方向右移的距离为 1,竖直移动的距离由玩家控制。如果点击屏幕,小鸟就会上升一定高度 X,每个单位时间可以点击多次,效果叠加;如果不点击屏幕,小鸟就会下降一定高度 Y。小鸟位于横坐标方向不同位置时,上升的高度 X和下降的高度 Y可能互不相同。
- 小鸟高度等于0或者小鸟碰到管道时,游戏失败。小鸟高度为 m时,无法再上升。
现在,请你判断是否可以完成游戏。如果可以,输出最少点击屏幕数;否则,输出小鸟最多可以通过多少个管道缝隙。
Input
第 1行有 3个整数 n,m,k,分别表示游戏界面的长度,高度和水管的数量,每两个整数之间用一个空格隔开;
接下来的 n行,每行 2个用一个空格隔开的整数 X和 Y,依次表示在横坐标位置 0~n-1上玩家点击屏幕后,小鸟在下一位置上升的高度 X,以及在这个位置上玩家不点击屏幕时,小鸟在下一位置下降的高度 Y。
接下来 k行,每行 3个整数 P,L,H,每两个整数之间用一个空格隔开。每行表示一个管道,其中 P表示管道的横坐标,L表示此管道缝隙的下边沿高度为 L,H表示管道缝隙上边沿的高度(输入数据保证 P各不相同,但不保证按照大小顺序给出)。
Output
第一行,包含一个整数,如果可以成功完成游戏,则输出 1,否则输出 0。
第二行,包含一个整数,如果第一行为 1,则输出成功完成游戏需要最少点击屏幕数,否则,输出小鸟最多可以通过多少个管道缝隙。
Sample Input
Input I: 10 10 6 3 9 9 9 1 2 1 3 1 2 1 1 2 1 2 1 1 6 2 2 1 2 7 5 1 5 6 3 5 7 5 8 8 7 9 9 1 3 Input II: 10 10 4 1 2 3 1 2 2 1 8 1 8 3 2 2 1 2 1 2 2 1 2 1 0 2 6 7 9 9 1 4 3 8 10
Sample Output
Output I: 1 6 Output II: 0 3
HINT
【输入输出样例说明】
如下图所示,蓝色直线表示小鸟的飞行轨迹,红色直线表示管道。
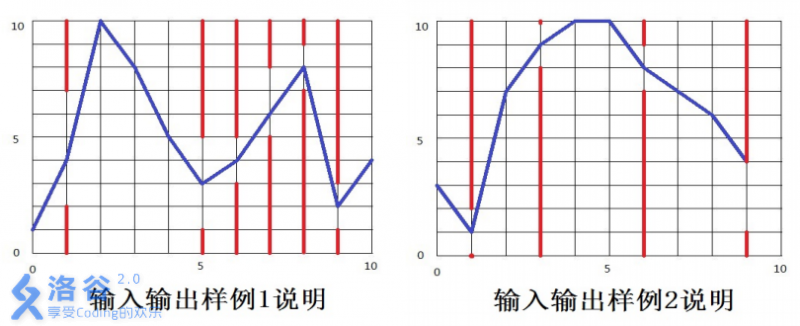
【数据范围】
对于 30%的数据:5≤n≤10,5≤m≤10,k=0,保证存在一组最优解使得同一单位时间最多点击屏幕 3次;
对于 50%的数据:5≤n≤20,5≤m≤10,保证存在一组最优解使得同一单位时间最多点击屏幕 3次;
对于 70%的数据:5≤n≤1000,5≤m≤100;
对于 100%的数据:5≤n≤10000,5≤m≤1000,0≤k<n,0<X<m,0<Y<m,0<P<n,0≤L<H ≤m,L+1<H。
Source
题解:
一道混合背包的好题。
如果对简单背包(0/1背包,完全背包,多重背包,混合背包)还不是很了解的小伙伴请戳这里:
有了这些基础知识,我们来分析问题:
其实一开始看题也挺蒙圈的,但是注意到了一句话:效果可以叠加。那脑子里就突然闪过一道光:既然可以叠加,那就相当于任意多物品选几件呗!背包啊!
正解的方向出来了。
因为题目中要求的是走到终点最少点击屏幕多少次,那么我们以此定义状态:(dp[i][j])表示走到(i)处(即横坐标为(i))、高度为(j)的时候,需要最少的点击量(点击量...)。
那么,向上跳就是完全背包的转移过程,向下落就是01背包的转移过程。
另外要注意,超过(m)的时候要特判,根据这个性质:数组的(m)要开二倍!即(2000)级别。
那么状态转移方程即为:
这个方程是完全背包的方程(当前位置跳和上一个位置跳)
这个方程是(m)溢出的特判。
这个方程是0/1背包的方程(跳还是不跳)
因为是向下跳,所以在选择跳的时候,第二维应该加上(y[i])。
统计答案的过程就是一个特判加标记的过程,在此不加赘述,请自行参看蒟蒻代码进行解决:
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxn=1e4+10;
const int maxm=1010*2;
int n,m,k,ans;
int x[maxn],y[maxn],up[maxn],down[maxn];
bool flag[maxn],q;
int dp[maxn][maxm];
//dp[i][j]表示横坐标为i时高度为j时的最小点击次数。
char *p1,*p2,buf[100000];
#define nc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++)
int read()
{
int x=0,f=1;
char ch=nc();
while(ch<48){if(ch=='-')f=-1;ch=nc();}
while(ch>47) x=(((x<<2)+x)<<1)+ch-48,ch=nc();
return x*f;
}
int main()
{
n=read(),m=read(),k=read();
for(int i=1;i<=n;i++)
{
x[i]=read();y[i]=read();
down[i]=1;
up[i]=m;
}
for(int i=1;i<=k;i++)
{
int a,b,c;
a=read(),b=read(),c=read();
flag[a]=1;
up[a]=c-1;
down[a]=b+1;
}
memset(dp,0x3f,sizeof(dp));
for(int i=1;i<=m;i++)
dp[0][i]=0;
//dp[i][j]表示横坐标为i时高度为j时的最小点击次数。
for(int i=1;i<=n;i++)
{
for(int j=1+x[i];j<=m+x[i];j++)
dp[i][j]=min(dp[i][j-x[i]]+1,dp[i-1][j-x[i]]+1);
for(int j=m+1;j<=m+x[i];j++)
dp[i][m]=min(dp[i][m],dp[i][j]);
for(int j=1;j<=m-y[i];j++)
dp[i][j]=min(dp[i][j],dp[i-1][j+y[i]]);
for(int j=1;j<=down[i]-1;j++)
dp[i][j]=dp[0][0];
for(int j=up[i]+1;j<=m;j++)
dp[i][j]=dp[0][0];
}
ans=dp[0][0];
for(int i=1;i<=m;i++)
ans=min(ans,dp[n][i]);
if(ans<dp[0][0])
{
printf("1
%d",ans);
return 0;
}
else
{
int i;
for(i=n;i>=1;i--)
{
for(int j=1;j<=m;j++)
if(dp[i][j]<dp[0][0])
{
q=1;
break;
}
if(q)
break;
}
ans=0;
for(int j=1;j<=i;j++)
if(flag[j])
ans++;
printf("0
%d",ans);
return 0;
}
}