CF1065F Up and Down the Tree
题目描述
You are given a tree with nn vertices; its root is vertex 11 . Also there is a token, initially placed in the root. You can move the token to other vertices. Let's assume current vertex of token is vv , then you make any of the following two possible moves:
- move down to any leaf in subtree of vv ;
- if vertex vv is a leaf, then move up to the parent no more than kk times. In other words, if h(v)h(v) is the depth of vertex vv (the depth of the root is 00 ), then you can move to vertex tot**o such that tot**o is an ancestor of vv and h(v) - k le h(to)h(v)−k≤h(t**o) .
Consider that root is not a leaf (even if its degree is 11 ). Calculate the maximum number of different leaves you can visit during one sequence of moves.
输入格式
The first line contains two integers nn and kk ( 1 le k < n le 10^61≤k<n≤106 ) — the number of vertices in the tree and the restriction on moving up, respectively.
The second line contains n - 1n−1 integers p_2, p_3, dots, p_np2,p3,…,p**n , where p_ip**i is the parent of vertex ii .
It is guaranteed that the input represents a valid tree, rooted at 11 .
输出格式
Print one integer — the maximum possible number of different leaves you can visit.
题意翻译
你有一棵带有n个结点的树，根是结点1。有一个标记，最初在根结点处。你可以将标记移动到其他结点处。假设标记当前所在结点为v，你可以做出以下两种操作：
将标记移动到v子树的任一叶子处。
如果是结点v为叶子，则将标记向根移动不超过 k 次。换句话说，如果 h(v) 为结点 v 的深度 (根的深度为0），你可以将其移动到顶点 to （ to 为 v 祖先） 并且 h(v)−k≤h(to)。
根不是叶子（即使它的度数是 1）。计算最多能访问多少叶子。
输入格式：
第一行包含两个整数 n 和 k (1<k<n≤10^6) --- 树中的顶点数和向上移动的限制。
第二行包含 n-1个整数 第i个整数表示结点i+1的父亲 输入保证树合法，根为1。
输出格式：
输出一个整数，表示可以访问的最大叶子数。
输入输出样例
输入 #1复制
输出 #1复制
输入 #2复制
输出 #2复制
说明/提示
The graph from the first example:
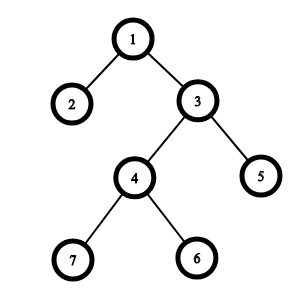One of the optimal ways is the next one: 1
ightarrow 2
ightarrow 1
ightarrow 5
ightarrow 3
ightarrow 7
ightarrow 4
ightarrow 61→2→1→5→3→7→4→6 .
The graph from the second example:
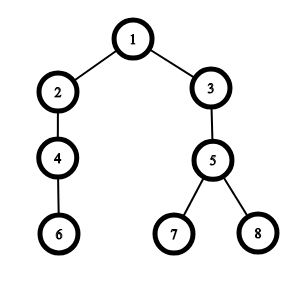One of the optimal ways is the next one: 1
ightarrow 7
ightarrow 5
ightarrow 81→7→5→8 . Note that there is no way to move from 66 to 77 or 88 and vice versa.
题解：
2019.10.28模拟赛T3骗分场
一开始发现暴力打起来很麻烦，正解不会。那么想到骗分。很显然，它求最多的可达叶子节点个数，那么会有很大的可能答案是所有叶子节点的个数。当然，这是过不了样例的。但是实测证明直觉很正确，骗到了60分（逃）
正解是树形DP。
在我个人的理解中，树形DP其实就是把一个节点的信息向上回溯统计得到答案的一类DP题。
那么我们分析一下思路：很显然，根据贪心原则，我们在从1号点选择往下走的时候，当然是挑选可达叶子节点最多的一棵子树来走。就是要看这个叶子节点往上跳能到达的节点中，相连叶子节点最多的点。
显然，统计的量就是(size[i])表示(i)节点的可达叶子节点的数量。
为了维护这个东西，我们继续统计两个量：第一个就是离某点最近的叶子节点的深度，定义为(near[i])，并且统计所有节点的正常深度(deep[i])。
那么，根据题意有：
那么我们只需要深搜处理出这几个数组，然后从底到上进行搜索求解更新即可。
代码：
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1e6+10;
const int INF=1e9;
int n,k;
int tot,head[maxn],nxt[maxn<<1],to[maxn<<1];
int deep[maxn],size[maxn],low[maxn];
bool v[maxn];
void add(int x,int y)
{
to[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void dfs1(int x,int d)
{
deep[x]=d;
low[x]=INF;
if(!v[x])
low[x]=d;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
dfs1(y,d+1);
low[x]=min(low[x],low[y]);
}
}
void dfs2(int x)
{
if(!v[x])
size[x]=1;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
dfs2(y);
if(low[y]-deep[x]<=k)
{
size[x]+=size[y];
size[y]=0;
}
}
}
int getsum(int x)
{
int ret=0;
for(int i=head[x];i;i=nxt[i])
ret=max(ret,getsum(to[i]));
return ret+=size[x];
}
int main()
{
scanf("%d%d",&n,&k);
for(int i=2;i<=n;i++)
{
int a;
scanf("%d",&a);
add(a,i);
v[a]=1;
}
dfs1(1,0);
dfs2(1);
printf("%d",getsum(1));
return 0;
}