CF938D Buy a Ticket
题目描述
Musicians of a popular band "Flayer" have announced that they are going to "make their exit" with a world tour. Of course, they will visit Berland as well.
There are nn cities in Berland. People can travel between cities using two-directional train routes; there are exactly mm routes, ii -th route can be used to go from city v_{i}v**i to city u_{i}u**i (and from u_{i}u**i to v_{i}v**i ), and it costs w_{i}w**i coins to use this route.
Each city will be visited by "Flayer", and the cost of the concert ticket in ii -th city is a_{i}a**i coins.
You have friends in every city of Berland, and they, knowing about your programming skills, asked you to calculate the minimum possible number of coins they have to pay to visit the concert. For every city ii you have to compute the minimum number of coins a person from city ii has to spend to travel to some city jj (or possibly stay in city ii ), attend a concert there, and return to city ii (if j≠ij≠i ).
Formally, for every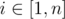 
you have to calculate 
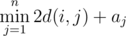, where d(i,j)d(i,j) is the minimum number of coins you have to spend to travel from city ii to city jj . If there is no way to reach city jj from city ii , then we consider d(i,j)d(i,j) to be infinitely large.
输入格式
The first line contains two integers nn and mm ( 2<=n<=2·10^{5}2<=n<=2⋅105 , 1<=m<=2·10^{5}1<=m<=2⋅105 ).
Then mm lines follow, ii -th contains three integers v_{i}v**i , u_{i}u**i and w_{i}w**i ( 1<=v_{i},u_{i}<=n,v_{i}≠u_{i}1<=v**i,u**i<=n,v**i≠u**i , 1<=w_{i}<=10^{12}1<=w**i<=1012 ) denoting ii -th train route. There are no multiple train routes connecting the same pair of cities, that is, for each (v,u)(v,u) neither extra (v,u)(v,u) nor (u,v)(u,v) present in input.
The next line contains nn integers a_{1},a_{2},... a_{k}a1,a2,... a**k ( 1<=a_{i}<=10^{12}1<=a**i<=1012 ) — price to attend the concert in ii -th city.
输出格式
Print nn integers. ii -th of them must be equal to the minimum number of coins a person from city ii has to spend to travel to some city jj (or possibly stay in city ii ), attend a concert there, and return to city ii (if j≠ij≠i ).
题意翻译
流行乐队“Flayer”将在n个城市开演唱会 这n个城市的人都想去听演唱会 每个城市的票价不同 于是这些人就想是否能去其他城市听演唱会更便宜（去要路费的） 输入格式： 第一行包含两个整数n和m 接下来m行 每行三个数 u v k 表示u城市到v城市要k元 接下来n个数 表每个城市的票价
感谢@凉凉 提供的翻译
输入输出样例
输入 #1复制
输出 #1复制
输入 #2复制
输出 #2复制
题解：
这道题稍微有一点歧义（我是说翻译）。
正常人看这个翻译，都不会考虑返程的情况，即不会把路径乘以2.这是可以理解的。因为翻译上确实没有说看完演唱会还要回来。但是原题上有很清晰的说明：(min^n_{j=1}2d(i,j)+a_j)。
我个人认为，看了这个式子之后，整个题的正解就差不多出来了。
我们暴力的想法就是：对每一个点跑单源最短路，然后统计最短的。但这道题的数据范围显然不支持这种思路：即使你用任意的最短路算法，加各种优化甚至卡常，都卡不过这个数据范围。
我是看过英语题面之后才看明白正解的思路的：我们发现：这题的数据范围是标准的跑一遍最短路的数据范围。所以我们把思路向只跑一遍最短路靠拢。根据上面的式子，我们发现，只要我们再把每个点的点权也包含进最短路算法的求解范围，那么就完全可以用一次最短路算法解决这个问题。然后我们想到把点权化边权，但这并不能保证原图的正确性（这是显然的）。
在我们迷之蒙圈不知干啥的时候，请让我来介绍一下正解。
建立虚拟源点。
这的确是一种好用的小技巧。前面的两路大神也解释的比较清晰。但是作为一名蒟蒻，我在第一次接触到这个技巧的时候还是蒙圈了。所以我来用对新手友好的方式解释一下这种思路。
设想一下，现在有一张图，源点是确定的，我们不考虑路径上的点权，只考虑终点的点权（注意，这是使用虚拟源点法的一个重要前提！）。那么，我们就可以在每个点上再引出一条边，这条边的边权就是这个点的点权。这样的化，我们就相当于多走了一条边，但是答案依然是正确的（因为那条边就是那个点权）。
可是，这样做会导致一个后遗症：终点不再确定。
怎么解决这个问题呢？很好办，我们把所有边的“新加出”的这条边的去向汇成一个点，这个点就是我们所说的“虚拟源点”。那么，我们从这个点开始跑最短路，所得出的每个点的答案就是真正的答案。
画个图应该会很好想。
看代码可能会更好想：
#include<cstdio>
#include<queue>
#include<cstring>
#define ll long long
using namespace std;
const int maxn=2*1e5+1;
priority_queue<pair<ll,int> >q;
int n,m;
int head[maxn],nxt[maxn*3],to[maxn*3],tot,v[maxn];
ll val[maxn*3];
ll dist[maxn];
void add(int x,int y,ll z)
{
to[++tot]=y;
val[tot]=z;
nxt[tot]=head[x];
head[x]=tot;
}
void dijkstra()
{
memset(dist,0x3f,sizeof(dist));
dist[0]=0;
q.push(make_pair(0,0));
while(!q.empty())
{
int x=q.top().second;
if(v[x])
{
q.pop();
continue;
}
x=q.top().second;q.pop();v[x]=1;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(dist[y]>dist[x]+val[i])
dist[y]=dist[x]+val[i],q.push(make_pair(-dist[y],y));
}
}
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
{
int u,v;ll w;
scanf("%d%d%lld",&u,&v,&w);
add(u,v,w * 2);
add(v,u,w * 2);
}
for(int i=1;i<=n;i++)
{
ll w;
scanf("%lld",&w);
add(0,i,w);
}
dijkstra();
for(int i=1;i<=n;i++)
printf("%lld ",dist[i]);
return 0;
}
注意：开Longlong，边权要乘二倍。