洛谷 P2146 [NOI2015]软件包管理器
题目描述
Linux用户和OSX用户一定对软件包管理器不会陌生。通过软件包管理器,你可以通过一行命令安装某一个软件包,然后软件包管理器会帮助你从软件源下载软件包,同时自动解决所有的依赖(即下载安装这个软件包的安装所依赖的其它软件包),完成所有的配置。Debian/Ubuntu使用的apt-get,Fedora/CentOS使用的yum,以及OSX下可用的homebrew都是优秀的软件包管理器。
你决定设计你自己的软件包管理器。不可避免地,你要解决软件包之间的依赖问题。如果软件包A依赖软件包B,那么安装软件包A以前,必须先安装软件包B。同时,如果想要卸载软件包B,则必须卸载软件包A。现在你已经获得了所有的软件包之间的依赖关系。而且,由于你之前的工作,除0号软件包以外,在你的管理器当中的软件包都会依赖一个且仅一个软件包,而0号软件包不依赖任何一个软件包。依赖关系不存在环(若有m(m≥2)个软件包A1,A2,A3,⋯,Am,其中A1依赖A2,A2依赖A3,A3依赖A4,……,A[m-1]依赖Am,而Am依赖A1,则称这m个软件包的依赖关系构成环),当然也不会有一个软件包依赖自己。
现在你要为你的软件包管理器写一个依赖解决程序。根据反馈,用户希望在安装和卸载某个软件包时,快速地知道这个操作实际上会改变多少个软件包的安装状态(即安装操作会安装多少个未安装的软件包,或卸载操作会卸载多少个已安装的软件包),你的任务就是实现这个部分。注意,安装一个已安装的软件包,或卸载一个未安装的软件包,都不会改变任何软件包的安装状态,即在此情况下,改变安装状态的软件包数为0。
输入格式
从文件manager.in中读入数据。
输入文件的第1行包含1个整数n,表示软件包的总数。软件包从0开始编号。
随后一行包含n−1个整数,相邻整数之间用单个空格隔开,分别表示1,2,3,⋯,n−2,n−1号软件包依赖的软件包的编号。
接下来一行包含1个整数q,表示询问的总数。之后q行,每行1个询问。询问分为两种:
install x:表示安装软件包x
uninstall x:表示卸载软件包x
你需要维护每个软件包的安装状态,一开始所有的软件包都处于未安装状态。
对于每个操作,你需要输出这步操作会改变多少个软件包的安装状态,随后应用这个操作(即改变你维护的安装状态)。
输出格式
输出到文件manager.out中。
输出文件包括q行。
输出文件的第i行输出1个整数,为第i步操作中改变安装状态的软件包数。
输入输出样例
输入 #1复制
输出 #1复制
输入 #2复制
输出 #2复制
说明/提示
【样例说明 1】
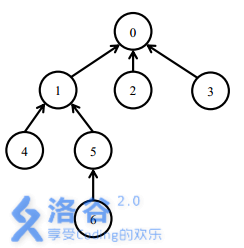
一开始所有的软件包都处于未安装状态。
安装5号软件包,需要安装0,1,5三个软件包。
之后安装6号软件包,只需要安装6号软件包。此时安装了0,1,5,6四个软件包。
卸载1号软件包需要卸载1,5,6三个软件包。此时只有0号软件包还处于安装状态。
之后安装4号软件包,需要安装1,4两个软件包。此时0,1,4处在安装状态。最后,卸载0号软件包会卸载所有的软件包。`
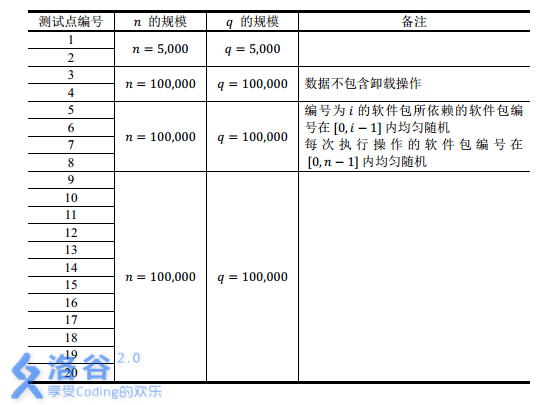
【数据范围】
【时限1s,内存512M】
题解:
一道树链剖分的模板题。
关于树链剖分的讲解请戳这里:
这道题难点有二:
第一个是读题,我们必须在读题之后明白这是一棵树,并且知道:安装一个软件就相当于安装这个点到根节点的所有未被安装的软件。卸载一个软件就是卸载以这个软件为根节点的子树的所有软件。
第二个是线段树的操作:我们知道线段树是用于区间操作的一种数据结构,那么这道题的区间修改,在线段树的相关题型中,又有一个名字:区间赋值。针对于这种区间赋值的线段树的题目,我们需要注意建树和打lazy标记时的相关信息的维护。比如,建树的时候lazy标记要置成-1。(这个时候的lazy数组属于标记数组,你愿意的话只要不设置成1设置啥都行)pushdown的时候一定要判一下当前的lazy是否为-1!(如果是就不能下传,要不然会导致下传的两个子节点的lazy值错误)。
剩下的就随便敲敲模板就成了。
上代码:
#include<cstdio>
#include<algorithm>
#define lson pos<<1
#define rson pos<<1|1
using namespace std;
const int maxn=1e5+1;
int n,q,tot,cnt;
int head[maxn],nxt[maxn<<1],to[maxn<<1];
int deep[maxn],fa[maxn],size[maxn],son[maxn];
int id[maxn],top[maxn];
int tree[maxn<<2],lazy[maxn<<2];
char s[100];
void add(int x,int y)
{
to[++tot]=y;
nxt[tot]=head[x];
head[x]=tot;
}
void dfs1(int x,int f)
{
deep[x]=deep[f]+1;
fa[x]=f;
size[x]=1;
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y==f)
continue;
dfs1(y,x);
size[x]+=size[y];
if(!son[x]||size[y]>size[son[x]])
son[x]=y;
}
}
void dfs2(int x,int t)
{
top[x]=t;
id[x]=++cnt;
if(!son[x])
return;
dfs2(son[x],t);
for(int i=head[x];i;i=nxt[i])
{
int y=to[i];
if(y==fa[x]||y==son[x])
continue;
dfs2(y,y);
}
}
void build(int pos,int l,int r)
{
lazy[pos]=-1;
int mid=(l+r)>>1;
if(l==r)
return;
build(lson,l,mid);
build(rson,mid+1,r);
}
void mark(int pos,int l,int r,int k)
{
tree[pos]=(r-l+1)*k;
lazy[pos]=k;
}
void pushdown(int pos,int l,int r)
{
int mid=(l+r)>>1;
if(lazy[pos]==-1) return;
mark(lson,l,mid,lazy[pos]);
mark(rson,mid+1,r,lazy[pos]);
lazy[pos]=-1;
}
void update(int pos,int l,int r,int x,int y,int k)
{
int mid=(l+r)>>1;
if(x<=l && r<=y)
{
mark(pos,l,r,k);
return;
}
pushdown(pos,l,r);
if(x<=mid)
update(lson,l,mid,x,y,k);
if(y>mid)
update(rson,mid+1,r,x,y,k);
tree[pos]=tree[lson]+tree[rson];
}
void upd_chain(int x,int y,int k)
{
while(top[x]!=top[y])
{
if(deep[top[x]]<deep[top[y]])
swap(x,y);
update(1,1,n,id[top[x]],id[x],k);
x=fa[top[x]];
}
if(deep[x]<deep[y])
swap(x,y);
update(1,1,n,id[y],id[x],k);
}
void upd_subtree(int x,int k)
{
update(1,1,n,id[x],id[x]+size[x]-1,k);
}
int main()
{
scanf("%d",&n);
for(int i=2;i<=n;i++)
{
int x;
scanf("%d",&x);x++;
add(x,i);
add(i,x);
}
dfs1(1,0);
dfs2(1,1);
build(1,1,n);
scanf("%d",&q);
while(q--)
{
int x;
int t=tree[1];
scanf("%s",s+1);
scanf("%d",&x);x++;
if(s[1]=='i')
{
upd_chain(1,x,1);
printf("%d
",abs(t-tree[1]));
}
else
{
upd_subtree(x,0);
printf("%d
",abs(t-tree[1]));
}
}
return 0;
}