转载:火烫火烫的
个人觉得BP反向传播是深度学习的一个基础,所以很有必要把反向传播算法好好学一下
得益于一步一步弄懂反向传播的例子这篇文章,给出一个例子来说明反向传播
不过是英文的,如果你感觉不好阅读的话,优秀的国人已经把它翻译出来了。
一步一步弄懂反向传播的例子(中文翻译)
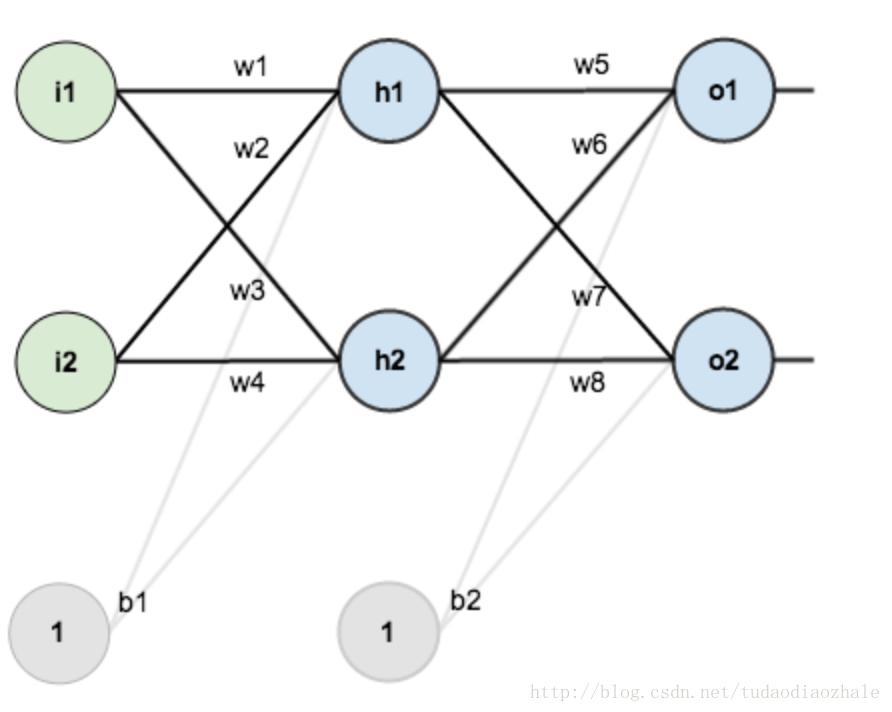
然后我使用了那个博客的图片。这次的目的主要是对那个博客的一个补充。但是首先我觉得先用面向过程的思想来实现一遍感觉会好一点。
随便把文中省略的公式给大家给写出来。大家可以先看那篇博文

1 import numpy as np 2 3 # "pd" 偏导 4 def sigmoid(x): 5 return 1 / (1 + np.exp(-x)) 6 7 def sigmoidDerivationx(y): 8 return y * (1 - y) 9 10 11 if __name__ == "__main__": 12 #初始化 13 bias = [0.35, 0.60] 14 weight = [0.15, 0.2, 0.25, 0.3, 0.4, 0.45, 0.5, 0.55] 15 output_layer_weights = [0.4, 0.45, 0.5, 0.55] 16 i1 = 0.05 17 i2 = 0.10 18 target1 = 0.01 19 target2 = 0.99 20 alpha = 0.5 #学习速率 21 numIter = 10000 #迭代次数 22 for i in range(numIter): 23 #正向传播 24 neth1 = i1*weight[1-1] + i2*weight[2-1] + bias[0] 25 neth2 = i1*weight[3-1] + i2*weight[4-1] + bias[0] 26 outh1 = sigmoid(neth1) 27 outh2 = sigmoid(neth2) 28 neto1 = outh1*weight[5-1] + outh2*weight[6-1] + bias[1] 29 neto2 = outh2*weight[7-1] + outh2*weight[8-1] + bias[1] 30 outo1 = sigmoid(neto1) 31 outo2 = sigmoid(neto2) 32 print(str(i) + ", target1 : " + str(target1-outo1) + ", target2 : " + str(target2-outo2)) 33 if i == numIter-1: 34 print("lastst result : " + str(outo1) + " " + str(outo2)) 35 #反向传播 36 #计算w5-w8(输出层权重)的误差 37 pdEOuto1 = - (target1 - outo1) 38 pdOuto1Neto1 = sigmoidDerivationx(outo1) 39 pdNeto1W5 = outh1 40 pdEW5 = pdEOuto1 * pdOuto1Neto1 * pdNeto1W5 41 pdNeto1W6 = outh2 42 pdEW6 = pdEOuto1 * pdOuto1Neto1 * pdNeto1W6 43 pdEOuto2 = - (target2 - outo2) 44 pdOuto2Neto2 = sigmoidDerivationx(outo2) 45 pdNeto1W7 = outh1 46 pdEW7 = pdEOuto2 * pdOuto2Neto2 * pdNeto1W7 47 pdNeto1W8 = outh2 48 pdEW8 = pdEOuto2 * pdOuto2Neto2 * pdNeto1W8 49 50 # 计算w1-w4(输出层权重)的误差 51 pdEOuto1 = - (target1 - outo1) #之前算过 52 pdEOuto2 = - (target2 - outo2) #之前算过 53 pdOuto1Neto1 = sigmoidDerivationx(outo1) #之前算过 54 pdOuto2Neto2 = sigmoidDerivationx(outo2) #之前算过 55 pdNeto1Outh1 = weight[5-1] 56 pdNeto2Outh2 = weight[7-1] 57 58 pdEOuth1 = pdEOuto1 * pdOuto1Neto1 * pdNeto1Outh1 + pdEOuto2 * pdOuto2Neto2 * pdNeto1Outh1 59 pdOuth1Neth1 = sigmoidDerivationx(outh1) 60 pdNeth1W1 = i1 61 pdNeth1W2 = i2 62 pdEW1 = pdEOuth1 * pdOuth1Neth1 * pdNeth1W1 63 pdEW2 = pdEOuth1 * pdOuth1Neth1 * pdNeth1W2 64 pdNeto1Outh2 = weight[6-1] 65 pdNeto2Outh2 = weight[8-1] 66 pdOuth2Neth2 = sigmoidDerivationx(outh2) 67 pdNeth2W3 = i1 68 pdNeth2W4 = i2 69 pdEOuth2 = pdEOuto1 * pdOuto1Neto1 * pdNeto1Outh2 + pdEOuto2 * pdOuto2Neto2 * pdNeto2Outh2 70 pdEW3 = pdEOuth2 * pdOuth2Neth2 * pdNeth2W3 71 pdEW4 = pdEOuth2 * pdOuth2Neth2 * pdNeth2W4 72 #权重更新 73 weight[1-1] = weight[1-1] - alpha * pdEW1 74 weight[2-1] = weight[2-1] - alpha * pdEW2 75 weight[3-1] = weight[3-1] - alpha * pdEW3 76 weight[4-1] = weight[4-1] - alpha * pdEW4 77 weight[5-1] = weight[5-1] - alpha * pdEW5 78 weight[6-1] = weight[6-1] - alpha * pdEW6 79 weight[7-1] = weight[7-1] - alpha * pdEW7 80 weight[8-1] = weight[8-1] - alpha * pdEW8 81 # print(weight[1-1]) 82 # print(weight[2-1]) 83 # print(weight[3-1]) 84 # print(weight[4-1]) 85 # print(weight[5-1]) 86 # print(weight[6-1]) 87 # print(weight[7-1]) 88 # print(weight[8-1])
不知道你是否对此感到熟悉一点了呢?反正我按照公式实现一遍之后深有体会,然后用向量的又写了一次代码。
接下来我们要用向量来存储这些权重,输出结果等,因为如果我们不这样做,你看上面的例子就知道我们需要写很多w1,w2等,这要是参数一多就很可怕。
这些格式我是参考吴恩达的格式,相关课程资料->吴恩达深度学习视频。
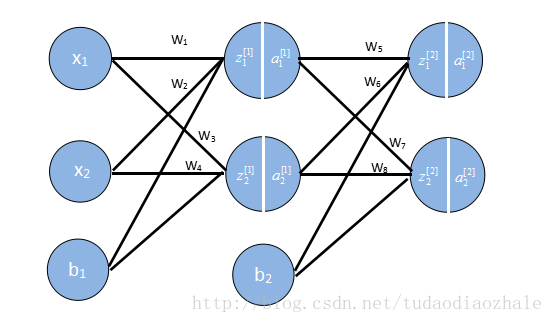
1 import numpy as np 2 3 def sigmoid(x): 4 return 1 / (1 + np.exp(-x)) 5 def sigmoidDerivationx(y): 6 return y * (1 - y) 7 8 9 if __name__ == '__main__': 10 # 初始化一些参数 11 alpha = 0.5 12 numIter = 1000000 #迭代次数 13 w1 = [[0.15, 0.20], [0.25, 0.30]] # Weight of input layer 14 w2 = [[0.40, 0.45], [0.50, 0.55]] 15 # print(np.array(w2).T) 16 b1 = 0.35 17 b2 = 0.60 18 x = [0.05, 0.10] 19 y = [0.01, 0.99] 20 # 前向传播 21 z1 = np.dot(w1, x) + b1 # dot函数是常规的矩阵相乘 22 a1 = sigmoid(z1) 23 24 z2 = np.dot(w2, a1) + b2 25 a2 = sigmoid(z2) 26 for n in range(numIter): 27 # 反向传播 使用代价函数为C=1 / (2n) * sum[(y-a2)^2] 28 # 分为两次 29 # 一次是最后一层对前面一层的错误 30 31 delta2 = np.multiply(-(y-a2), np.multiply(a2, 1-a2)) 32 # for i in range(len(w2)): 33 # print(w2[i] - alpha * delta2[i] * a1) 34 #计算非最后一层的错误 35 # print(delta2) 36 delta1 = np.multiply(np.dot(np.array(w2).T, delta2), np.multiply(a1, 1-a1)) 37 # print(delta1) 38 # for i in range(len(w1)): 39 # print(w1[i] - alpha * delta1[i] * np.array(x)) 40 #更新权重 41 for i in range(len(w2)): 42 w2[i] = w2[i] - alpha * delta2[i] * a1 43 for i in range(len(w1)): 44 w1[i] = w1[i] - alpha * delta1[i] * np.array(x) 45 #继续前向传播,算出误差值 46 z1 = np.dot(w1, x) + b1 47 a1 = sigmoid(z1) 48 z2 = np.dot(w2, a1) + b2 49 a2 = sigmoid(z2) 50 print(str(n) + " result:" + str(a2[0]) + ", result:" +str(a2[1])) 51 # print(str(n) + " error1:" + str(y[0] - a2[0]) + ", error2:" +str(y[1] - a2[1]))
可以看到,用向量来表示的话代码就简短了非常多。但是用了向量化等的方法,如果不太熟,去看吴恩达深度学习的第一部分,再返过来看就能懂了。