复杂数据类型
三种
- 序列数据
- 图与网络
- 其他数据类型
挖掘序列数据
序列是事件的有序列表。根据事件的特征,序列数据可以分为三类:
-
时间序列数据:包含不同时间点重复测量得到的数值序列
-
本身具备的高维性、复杂性、动态性、高噪声特性以及容易达到大规模的特性,直接在时间序列上进行数据挖掘不但在储存和计算上要花费高昂代价而且可能会影响算法的准确性和可靠性。
-
时间序列的模式表示是一种对时间序列进行抽象和概括的特征表示方法,是在更高层次上对时间序列的重新描述。
-
时间序列的模式表示具有压缩数据、保持时间序列基本形态的功能,并且具有一定的除噪能力。
-
常用的时间序列模式表示方法主要包含:频域表示法、分段线性表示法、符号表示法以及主成分分析表示法等
-
趋势分析:自动回归集成的移动平均ARIMA、LTSM模型、自回归-
趋势或长期动向:指出时间序列随时间运动的大体方向
-
周期动向:趋势线或曲线的长期波动
-
季节变化:指几乎相同的模式出现于相继年份的对应季节
-
随机动向:刻画由于劳务争议或公司内部宣布的人事变化等偶然事件导致的随机变化
-
-
-
符号序列数据:由元素或事件的有序集组成,记录或未记录具体时间。
- 序列模式是一个存在于单个序列或一个序列集中的频繁子序列。
-
生物学序列
2、典型的维规约技术:
频域表示法:频域表示的基本思想是将时间序列从时域通过傅里叶变换或小波变换映射到频域,用很少的低频系数来代表原来的时间序列数据,这种方法虽然数据浓缩的效率很高,但是对噪声敏感,而且不直观
- DFT
- DWT
符号表示法
- 时间序列的符号化表示就是通过一些离散化方法将时间序列的连续实数值或者一段时间内的时间序列波形映射到有限的符号表上,将时间序列转换为有限符号的有序集合。
- 符号化表示的优点在于可以利用许多字符串研究领域的成果,缺点在于如何选择合适的离散化算法,解释符号的意义,以及定义符号之间的相似性度量。
主成分分析
-
主成分分析是一种常见的降维方法。在时间序列的模式表示中,通过对整个时间序列数据库的整体表示实现对整个时间序列数据库的特征提取和压缩。
-
其优点在于计算精度高且对噪声数据的鲁棒性强,但由于在奇异值分解过程中涉及到特征值计算,计算开销较大。
-
基于PCA的SVD
序列分类:
序列分类可以分为三类:
- 基于特征的分类:把序列转换成特征向量,然后使用传统的分类方法
- 基于序列距离的分类:其中度量序列之间相似性的距离函数决定分类的质量
- 基于模型的分类:使用HMM或其他统计学模型来对序列分类
对于时间序列或其他数据数据,用于符号序列的特征选择技术不能用于非离散化的时间序列数据。shapelets方法最能表示时间序列子序列为特征,取得了高质量的分类结果。
shapelets:
- 基于距离计算的时间序列分类方法,需要计算不同时间序列在整个序列上的相似性。然而,很多情况下不同类的时间序列在全局形状上的差异很微小且序列之间存在噪声,直接计算两个序列在全局上的相似性很难区分不同类的时间序列 。Shapelet是一种新的时间序列分类方法,由于时间序列在全局上的差异性不显著,因此通过比较Shapelet与完整时间序列之间的相似性能够突出序列之间的差异性。一个长度为L的Shapelet是一个有序的子序列,能够最大程度上区分不同类的时间序列数据 。
- 具体的计算方法是任取一段子序列,计算该子序列与样本的任意等长子序列的距离的最小值,记为该子序列与样本的距离,计算完子序列与所有样本的距离之后,设定一个划分点,将所有样本分类,根据标签计算划分之后信息增益最大的划分点的值。时间序列中的Shapelet是所有子序列中使划分前后信息增益最大的子序列,它可能是时间序列的训练数据中任一样本的任一子序列,因此其时间复杂度是很大的。
生物学序列比对
1)生物学序列分析比较、比对、索引和分析生物学序列,因而在生物信息学和现代生物学中起着至关重要的作用。
2)生物序列比对的问题描述如下
-
对于给定的两个或多个输入生物序列,识别具有长保守子序列的相似序列。
-
核苷酸:如果两个符号相同,则他们对齐
-
蛋白质:如果两个符号相同,或者一个开通过可能自然出现的替换从另一个得到,则他们对齐。
-
两种比对:局部比对和全局比对
-
对于核苷酸和蛋白质来说,插入、删除和置换在自然界以不同的概率出现。
- 置换矩阵:用于描述核苷酸或蛋白质的置换概率和插入、删除概率。
- 动态规划方法通常用于序列比对。
-
生物学序列分析的隐含尔科夫模型
-
马尔科夫链
-
隐马尔可夫模型常用方法:
- 前向算法:找出该模型中得到x的概率

-
Viterbi算法:找出通过模型的最可能路径
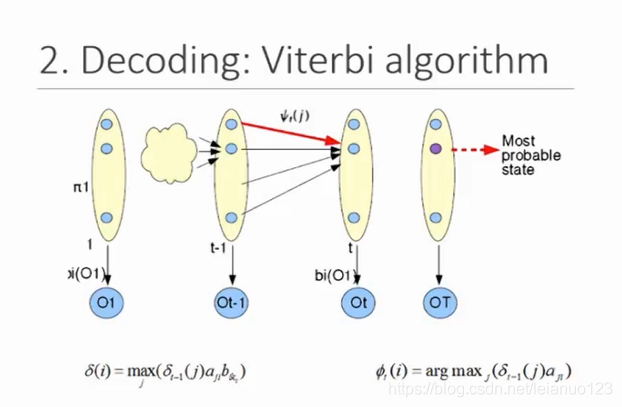
-
Baum-Welch算法:学习或调整模型的参数,以最好的解释训练序列集
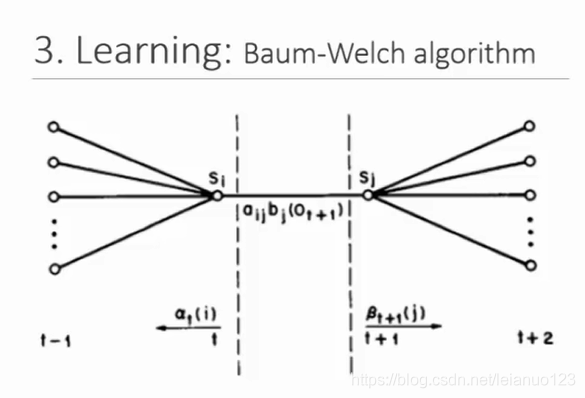
-