kdTree相关原理及c++实现

kdTree概念

        kd-tree或者k维树是计算机科学中使用的一种数据结构，用来组织表示k维空间中点的集合。它是一种带有其他约束条件的二分查找树。Kd-tree对于区间和近邻搜索十分有用。一般位于三维空间中的邻域搜索常用kd-tree，因此本文中所有的kd-tree都是三维的kd-tree。

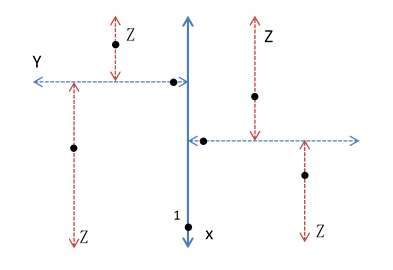
图一

        Kd-tree也是二叉树的一种，首先我们先选定一个维度用于第一次分类，如图一所示，我们先选择x维度方向作为分类方向，随机选取一个值使得小于该值的点位于左边，大于该值的点位于右边。在左右区域分别再对第二个维度进行分类，这里以y轴方向作为第二维度，同理根据y分类设置z轴方向为第三维度进行分类。

Kd-tree数据结构定义

Node-data:数据矢量，数据集中某个数据点，是n维矢量（总维度，unsigned int）

Range:空间矢量，该节点所代表的的空间范围（二维数组）

Split:整数，垂直于分割超平面的方向轴序号（int）

Left:k-d树，由位于该节点分割超平面左侧子空间内所有点构成的k-d树（tuple<list,int>）

Right:k-d树，由位于该节点分割超平面右侧子空间内所有点构成的k-d树（tuple<list,int>）

Parent:k-d树，父节点（auto）

Kd-tree优化

        方案一：Kd-tree通过不同维度划分数据，节点的选择显得尤为重要。我们可以想象一组点云，并不是完全随机离散的，只在某一维度上点云分布较为离散，其余维度相对集中。以三维空间为例，一组类似球状的点云在求每个方向的子节点能保证效率是最高的，但是数据接近一个平面时，在其中一个维度的划分就显得十分困难。

        解决方法：首先，对于点云分布不集中的那一维度来说，方差较大，我们可以通过最大方差法选择每次需要分类的维度，即在每次进行新的划分之前，我们通过判断方差选择在哪个维度上进行划分。

        方案二：为了保证每次选择的节点尽量位于中间位置，也就是让二叉树尽量为二叉平衡树，从而保证节点两侧的点云数目大致相等。

        解决方法：在选取节点前，我们对数据进行排序，选取中位数作为节点，这样就能保证两侧数据大致相等。

 PCL库c++源码

#include <iostream>
#include <pcl/point_types.h>
#include <pcl/io/pcd_io.h>
#include <pcl/kdtree/impl/kdtree_flann.hpp>
#include <pcl/kdtree/kdtree_flann.h>
#include <pcl/kdtree/kdtree.h>
#include <pcl/kdtree/io.h>
#include <pcl/kdtree/flann.h>
#include <pcl/search/kdtree.h>
#include <pcl/features/normal_3d.h>
#include <pcl/kdtree/impl/io.hpp>
#include <pcl/search/flann_search.h>
#include <pcl/surface/gp3.h>
//#include <pcl/visualization/pcl_visualizer.h>

int main(int argc, char* argv[])
{
    pcl::PointCloud<pcl::PointXYZ>::Ptr inCloud(new pcl::PointCloud<pcl::PointXYZ>);
    //construct a plane, the equation is x + y + z = 1
    for (float x = -1.0; x <= 1.0; x += 0.005)
    {
        for (float y = -1.0; y <= 1.0; y += 0.005)
        {
            pcl::PointXYZ cloud;

            cloud.x = x;
            cloud.y = y;
            cloud.z = 1 - x - y;
        
            inCloud->push_back(cloud);
        }
    }

    pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> ne;
    pcl::PointCloud<pcl::Normal>::Ptr pcNormal(new pcl::PointCloud<pcl::Normal>);
    pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>);
    tree->setInputCloud(inCloud);
    ne.setInputCloud(inCloud);
    ne.setSearchMethod(tree);
    ne.setKSearch(50);
    //ne->setRadiusSearch (0.03); 
    ne.compute(*pcNormal);

    pcl::PointCloud<pcl::PointXYZINormal>::Ptr cloud_with_normals(new pcl::PointCloud<pcl::PointXYZINormal>);
    pcl::concatenateFields(*inCloud, *pcNormal, *cloud_with_normals);

    pcl::io::savePCDFile("plane_cloud_out.pcd", *cloud_with_normals);

    return 0;
}

【 结束 】