集成学习 就是不断的通过数据子集形成新的规则,然后将这些规则合并。bagging和boosting都属于集成学习。集成学习的核心思想是通过训练形成多个分类器,然后将这些分类器进行组合。
所以归结为(1)训练样本数据如何选取?
(2)分类器如何合并?
一、bagging
bagging 通过将全部数据集中均匀随机有放回的挑选部分数据,然后利用挑选出的数据训练模型,然后再随机挑选部分数据训练一个新的模型,经过多次选择,形成多个模型,把每一个模型的值加权取平均就是bagging。
所以baging (1)样本数据均匀随机有放回的选取。
(2)分类器取均值。


左边这幅图,随机有放回的取5个数据,取五次,用三阶多项式拟合出5条曲线,看以看出这五条曲线基本上符合图像上点的走势。右边这幅图红色的曲线是用bagging实现的,蓝色的曲线是用四阶多项式实现的。在训练集上蓝色的拟合度优于红色,但是在测试集上红色要由于蓝色。可以看出baggin方法有很强的泛化能力。
二、boosting
boosting 不再均匀随机的挑选数据了,而是把重点放在那些不易进行分类的数据上或者是分错的数据上,增加分错样本的权值,然后再进行训练,经过多次样本数据选择,哪些最难分类的权值会不断增大,直到被分类正确。将形成的多个分类器进行投票,分类类别选择票数最多的那个。
boosting (1)调整权值,选择分错的样本。
(2)分类器合并采取投票的方式。
要理解boosting中如何增加分错样本的权重必须了解“误差”的概念。
误差:在已知样本分布的情况下,某一个样本x上的假设和真实值间不一致的概率。
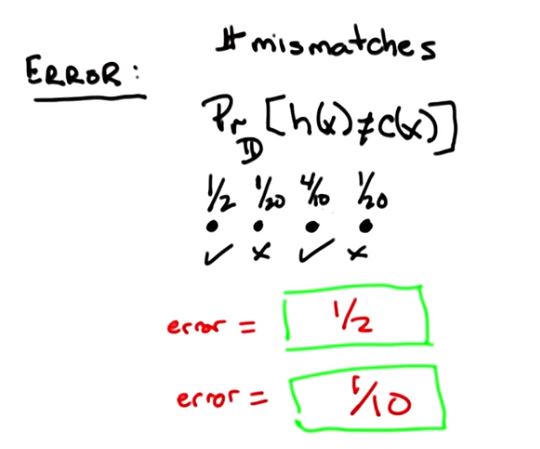
如上面这幅图,有四个点,分别出现的频率是1/2,1/20,4/10,1/20,所以由上面误差的概念,分错的概率为1/10。
所以样本出现的频率会影响误差,也就是样本的分布会随着权值的变化而变化。相比我们已经分对的样本,分错的样本获得正确结果的概率就越高。