今天看到挑战程序设计上有一题博弈叫阶梯博弈,可以另类表示成尼姆博弈,感觉很有趣,于是去看了想相关的博文。
参考了这篇博客:我谈阶梯博弈( Staircase Nim )。
阶梯博弈:博弈在一列阶梯上进行,每个阶梯上放着自然数个点,两个人进行阶梯博弈,每一步则是将一个集体上的若干个点
( >=1 )移到前面去,最后没有点可以移动的人输。
说的通俗点,是在一排阶梯上的博弈。 每列阶梯上都有若干个石子,如下图所示,两名玩家可以向左移动石子到相邻阶梯上,最后谁把所有石子移动到地面上谁就获胜。
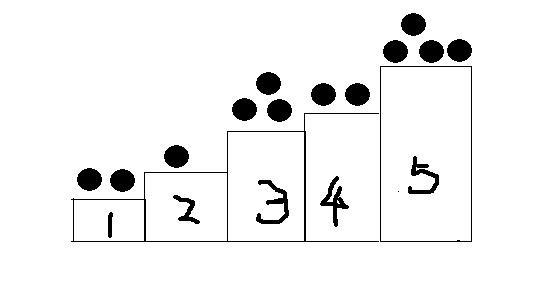
把阶梯都如图中所示标上序号(地面为0),那么我们可以把所有奇数堆石子看成N堆石子,然后当成尼姆博弈来求解。下面让我们来解释一下为什么可以这么写。
我们先按尼姆博弈的角度看这道题,设sum=a1^a2^.....an,如果当前的sum!=0,也就是先手必胜。那么先手就只对奇数堆进行操作,如果后一个人也对奇数堆进行操作,相当于在进行尼姆博弈。那么偶数堆的影响呢?假设后一个人对偶数堆进行操作将石子移动到奇数堆,企图改变先手的必胜态,但是下一次轮到先手时,只要将奇数堆里多出来的石子移动到偶数堆里去,就又恢复到了原来的状态,所以对偶数堆的操作并不会改变奇数堆的状态,也就不会影响到尼姆博弈的到过程,可以将偶数堆忽略。如果先手必败呢?同理,如果先手移动偶数堆,后手会从奇数堆移出相同数量的石子,没有影响,只要判断奇数堆做尼姆博弈的情况即可。
为什么是只对奇数堆做Nim就可以而不是偶数堆呢?因为如果是对偶数堆做Nim,对手移动奇数堆的石子到偶数堆,我们跟着移动这些石子到下一个奇数堆,那么最后是对手把这些石子移动到了0,我们不能继续跟着移动。那这样一来奇数堆就对偶数堆的Nim就有了影响,就不能只对偶数堆做Nim来比赛了。
例题一
POJ 1704 Georgia and Bob
题目链接:http://poj.org/problem?id=1704
题目大意:有一行排成直线的格子上放有n个棋子,如下图所示:
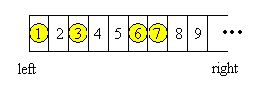
Georgia和Bob轮流选择一个棋子向左移动,每次可以移动一个及以上任意多格,但是不允许反超其他的棋子,也不允许将两个棋子放在同一个格子内。无法进行移动操作的一方失败,问谁会赢?
解题思路:阶梯博弈,当棋子有偶数个时,我们可以将棋子两两当成Nim中的一堆石子,两棋子中间的格子数为堆的石子数。如下图所示:
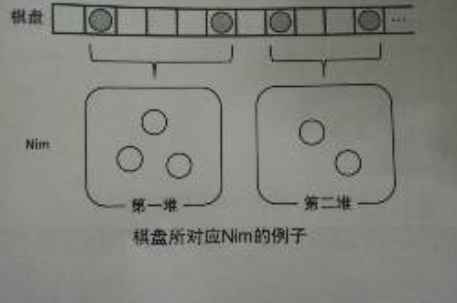
那就跟上面介绍的阶梯博弈一样了,把棋子组成的堆的石子数看成奇数列阶梯石子数,堆与堆之间的间隔看成偶数列阶梯的石子数,最终目的是把所有的石子都移到最右边(地面)。
当棋子有奇数个时,我们要进行特殊处理,将多出来的一个棋子与棋盘最左侧组成一堆,如下图所示:
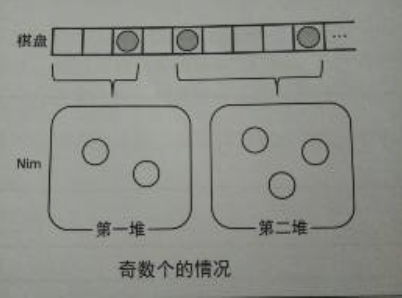
所以最后解法就像Nim一样对每堆的石子数进行异或求和,最后判断异或值如果不为0,则先手胜,反之后首胜。注意一下,题目给出的棋子位置不是从小到大给的,所以要自己排下序,坑。
代码:
1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 const int N=1e3+5; 5 int a[N]; 6 7 int main(){ 8 int T; 9 scanf("%d",&T); 10 while(T--){ 11 int n; 12 scanf("%d",&n); 13 for(int i=1;i<=n;i++){ 14 scanf("%d",&a[i]); 15 } 16 //n为奇数就将棋盘最左侧当成一个棋子 17 if(n%2==1) 18 a[++n]=0; 19 sort(a+1,a+1+n); 20 int sum=0; 21 for(int i=2;i<=n;i+=2){ 22 sum^=(a[i]-a[i-1]-1); 23 } 24 if(sum!=0) 25 puts("Georgia will win"); 26 else 27 puts("Bob will win"); 28 } 29 }
例题二
HDU 4315 Climbing the Hill
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4315
题目大意:山上有n个人,Alice和Bob轮流操作,每次可以选择一个人向上移动任意距离,但不能超过前面的人。山顶(坐标为0)可以站多个人,其他格子只能站一个人,在距离山顶第k远的位置的人时king,谁能先把king送上山顶谁就是获胜者。如下图为样例:
3 3
1 2 4
解题思路:这个题目跟上面的移动棋子的问题很像,如果没有king,那么解法就是一样的偶数时棋子两两成堆,奇数时令山顶与第一个人形成第一个区间(a[0]=-1),用Nim求解。但是多了king的话就需要多一些特殊判断,k==1时,Alice直接获胜,n为奇数且k==2时,因为谁先移动第一颗棋子到山顶谁就会输,除了没得选择谁都不会这么做,所以要把第一个区间距离-1(a[0]=-1+1=0)。
代码:
1 #include<cstdio> 2 const int N=1e3+5; 3 4 int a[N]; 5 6 int main(){ 7 int n,k; 8 while(~scanf("%d%d",&n,&k)){ 9 for(int i=1;i<=n;i++){ 10 scanf("%d",&a[i]); 11 } 12 13 if(k==1){ 14 puts("Alice"); 15 continue; 16 } 17 int sum=0; 18 //n为奇数,让第一个棋子与最顶上形成第一个区间 19 if(n%2==1){ 20 //k==2时,第一个区间距离-1 21 a[0]=-1+(k==2); 22 for(int i=1;i<=n;i+=2) 23 sum^=(a[i]-a[i-1]-1); 24 } 25 else{ 26 for(int i=2;i<=n;i+=2) 27 sum^=(a[i]-a[i-1]-1); 28 } 29 if(sum!=0) 30 puts("Alice"); 31 else 32 puts("Bob"); 33 } 34 }