C/C++判定是否为平方数以及由此引出的IEEE754（1）

本部分介绍相关背景知识

1、C语言的char, short, int, long, long long类型都是由C自身规定的，但是float, double, long double都是没有规定的（unspecified），但大多数平台上的实现遵从IEEE754标准（参见http://en.wikipedia.org/wiki/C_data_types）

（C99标准似乎规定了float对应IEC60559 single format，double对应IEC60559 double format，long double推荐实现为IEC60559 extended format，参见C99标准文档442页Annex F）

IEC60559应该是IEEE754的别名：

“该标准的全称为IEEE二进制浮点数算术标准（ANSI/IEEE Std 754-1985），又称IEC 60559:1989，微处理器系统的二进制浮点数算术（本来的编号是IEC 559:1989）”（http://zh.wikipedia.org/wiki/IEEE_754）

2、将一个int类型变量赋给double类型变量，是不会损失精度的；但是将一个long long类型变量赋给double，可能损失精度

IEEE754规定的double的格式是（参考http://en.wikipedia.org/wiki/Double_precision_floating-point_format）

sign是符号位，exponent是以无符号二进制表示的指数，上图表示的数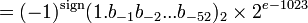，其中b_-1b_-2...b_-52就是图中fraction部分，e就是exponent。即

 

从此式可以看出，当e-1023>52时，两个相邻的double数之间的距离就不是1，而要>1。例如e-1023=53时，两个相邻的double数之间的距离是2，看下面的测试代码

#include <stdio.h>
int main(int argc, const char *argv[])
{
    double x = 9007199254740992ll;//2^53
    //x =  4503599627370496ll;//2^52
    for (int i = 0; i < 10; i++) {
        printf("%lf\n", x);
        x = x + 1.5;
    }
    return 0;
}
/*
输出是：
9007199254740992.000000
9007199254740994.000000
9007199254740996.000000
9007199254740998.000000
9007199254741000.000000
9007199254741002.000000
9007199254741004.000000
9007199254741006.000000
9007199254741008.000000
9007199254741010.000000
*/

每次x加1.5时，会找到最近的double值赋给x；如果是加1的话，这里10个数完全相同。

这里有一段话（来自http://stackoverflow.com/questions/4317988/ieee-754-floating-point-precision-how-much-error-is-allowed/4319151#4319151）

The IEEE-754 standard requires that so called "basic operations" (which include addition, multiplication, division and square root) are correctly rounded. This means that there is a unique allowed answer, and it is the closest representable floating-point number to the so-called "infinitely precise" result of the operation.

这里还有一段（来自http://stackoverflow.com/questions/14151740/sqrt-perfect-squares-and-floating-point-errors/14152959#14152959）

In IEEE 754 floating-point, if the double-precision value x is the square of a nonnegative representable number y (i.e. y*y == x and the computation of y*y does not involve any rounding, overflow, or underflow), then sqrt(x) will return y.

This is all because sqrt is required to be correctly-rounded by the IEEE 754 standard. That is, sqrt(x), forany x, will be the closest double to the actual square root of x. That sqrt works for perfect squares is a simple corollary of this fact.