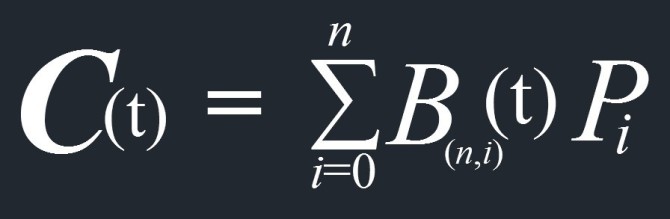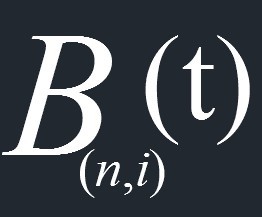在AutoCAD中生成贝塞尔曲线

贝赛尔曲线的定义 

贝塞尔曲线（Bézier curve）是由法国雷诺公司的设计师Pierre Bézier设计。它的具体定义如下：

　　　　

　　　　　　　

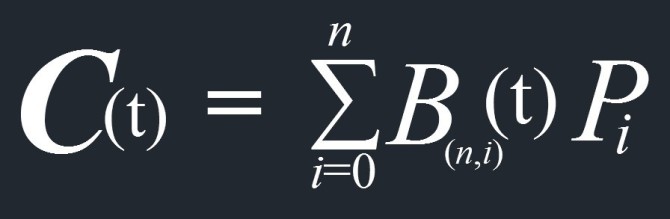
　　　　　　其中Pi（i=0,1,2,...n）称作曲线的控制向量，他们组成的连续多段线叫做曲线的控制多边形； t ∈[0，1]，即 t 从0连续变化到1时所生成的曲线就叫做贝赛尔曲线。而函数：

　　　　

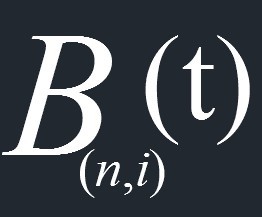
  叫做贝塞尔基函数（Bézier basis functions），也叫做伯恩斯坦多项式（Bernstein polynomials）它的定义如下：

其中n!=1*2*3*...*n 即n的阶乘函数。

参考：http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/bezier-construct.html

Bezier曲线的生成算法

 

在 http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/de-casteljau.html  介绍了一个生成Bezier曲线上点的算法：

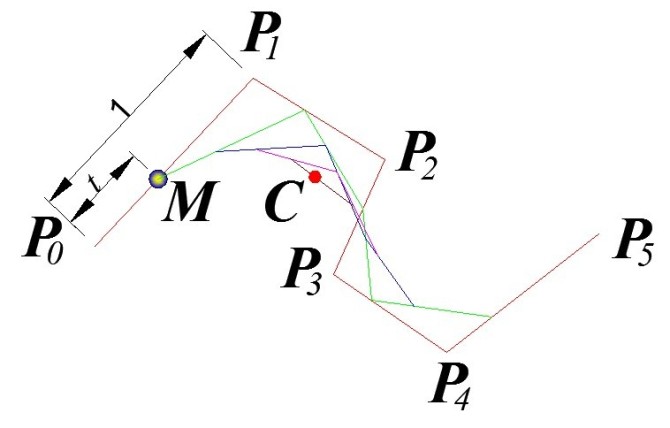
实现的代码

 

以下是在AutoCAD 2011 x64 中实现的代码，其他版本大同小异（vba实现）：

Sub bezier()
    Dim i As Long, j As Long, m As Long, n As Long
    Dim Coor As Variant, BezierPs() As Double, p(2) As Double
    Dim t As Double, s As Double, DeltaT As Double
    Dim SelecPoly As AcadSelectionSet
    Dim pointObj As AcadPoint, BezierL As AcadPolyline
    Dim pointID(10000000) As Double
    
    'delete all selection sets
    i = 0
    Do While ThisDrawing.SelectionSets.Count > 0
        ThisDrawing.SelectionSets.Item(i).Delete
        i = i + 1
    Loop

　'select a polyline in your drawing
    Set SelecPoly = ThisDrawing.SelectionSets.Add("ControlPoly")
    SelecPoly.SelectOnScreen
                                        
    'draw vertices of the Bezier Curve
    DeltaT = 0.001
    i = j = m = 0
    n = UBound(SelecPoly.Item(0).Coordinates) - 1
    Do While t <= 1 + DeltaT
        s = 1 - t
        Coor = SelecPoly.Item(0).Coordinates
        For i = 1 To n / 2
            For j = 0 To n - 2 * i Step 2
                Coor(j) = s * Coor(j) + t * Coor(j + 2)
                Coor(j + 1) = s * Coor(j + 1) + t * Coor(j + 3)
            Next
        Next
        p(0) = Coor(0): p(1) = Coor(1): p(2) = 0
        Set pointObj = ThisDrawing.ModelSpace.AddPoint(p)
        pointObj.Visible = True
        pointID(m) = pointObj.ObjectID32 'store the objectIDs of points
        m = m + 1
        t = t + DeltaT
    Loop
    
    'draw polyline to approximate Bezier Curve
    ReDim BezierPs(3 * m - 1)
    j = 0
    For i = 0 To 3 * m - 3 Step 3
        Set pointObj = ThisDrawing.ObjectIdToObject32(pointID(j))
        BezierPs(i) = pointObj.Coordinates(0)
        BezierPs(i + 1) = pointObj.Coordinates(1)
        BezierPs(i + 2) = pointObj.Coordinates(2)
        j = j + 1
    Next
    Set BezierL = ThisDrawing.ModelSpace.AddPolyline(BezierPs)
    
    'delete points
    For i = 0 To m - 1
        Set pointObj = ThisDrawing.ObjectIdToObject32(pointID(i))
        pointObj.Delete
    Next
End Sub

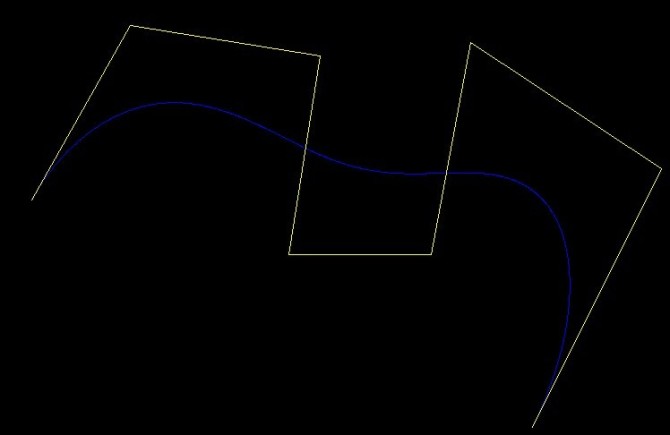
下面是生成的曲线效果图：