题目
分析
首先要画个草图观察规律,n = 1 ,2, 3 时,结果分别为1,2,5。分析当 n = 3时,BST的种类构成:根节点为1,根节点为2,根节点为3。当根节点为1时,有两种形态
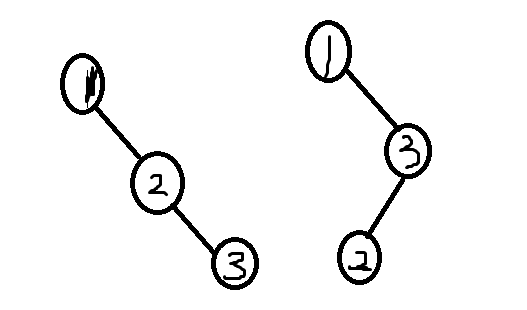
当根节点为2时,有一种形态

当根节点为3时,有两种形态
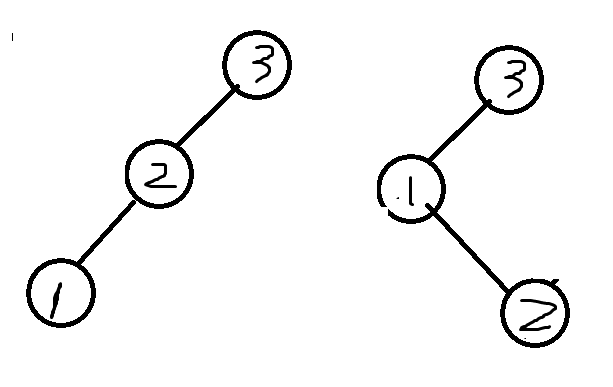
所以n为3时的BST数量为:根节点为1的BST个数 + 根节点为2的BST个数+根节点为3的BST个数。设dp【i】为从1—i组成的BST个数。dp[3] = dp[2] * dp[0] + dp[1] * dp[1]+
dp[0] * dp[2]
进而可得动态转移方程 dp[i] += dp[j - 1] * dp[i - j]
代码
1 class Solution { 2 public: 3 int numTrees(int n) { 4 vector<int>dp(n+1); 5 dp[0] = 1; 6 for(int i = 1;i <= n;i++){ 7 for(int j = i -1;j >= 0;j--){ 8 dp[i] += dp[j] * dp[i-j-1]; 9 } 10 } 11 return dp[n]; 12 } 13 };
时间复杂度O(N2),空间复杂度O(N)