题目
找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数,并且每种组合中不存在重复的数字。
分析
给定数字集合,找满足条件的组合。依旧是回溯问题,按照板子写就可,脑中一定要有回溯的搜索树的图形
代码
1 class Solution { 2 public: 3 vector<int>path; 4 vector<vector<int>>res; 5 void backtracking(int n,int k,int startIndex,int sum){ 6 if(path.size() == k ){ 7 if(sum == n){ 8 res.push_back(path); 9 } 10 return; 11 } 12 for(int i = startIndex; i <= 9;i++){ 13 path.push_back(i); 14 sum += i; 15 backtracking(n,k,i+1,sum); 16 sum -= path.back(); //或者sum -= i; 17 path.pop_back(); 18 } 19 } 20 vector<vector<int>> combinationSum3(int k, int n) { 21 backtracking(n,k,1,0); 22 return res; 23 } 24 };
优化搜索,进行剪枝
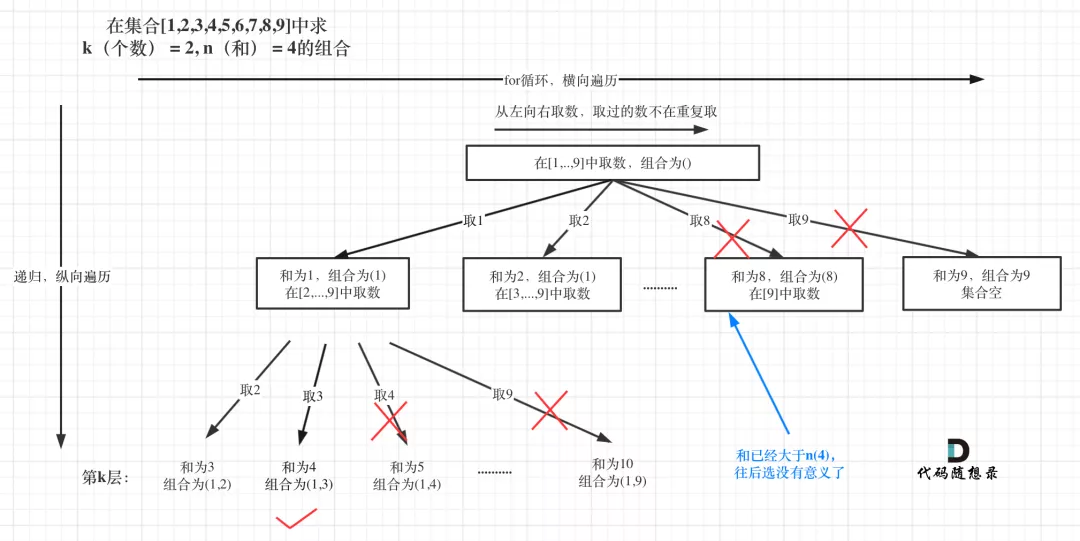
就是直接剪掉已选元素之和大于目标target的分支
1 class Solution { 2 public: 3 vector<int>path; 4 vector<vector<int>>res; 5 void backtracking(int n,int k,int startIndex,int sum){ 6 if(sum > n){ //剪枝优化 7 return; 8 } 9 if(path.size() == k ){ 10 if(sum == n){ 11 res.push_back(path); 12 } 13 return; 14 } 15 for(int i = startIndex; i <= 9;i++){ 16 path.push_back(i); 17 sum += i; 18 backtracking(n,k,i+1,sum); 19 sum -= path.back(); //或者sum -= i; 20 path.pop_back(); 21 } 22 } 23 vector<vector<int>> combinationSum3(int k, int n) { 24 backtracking(n,k,1,0); 25 return res; 26 } 27 };