算法基础——前缀和及差分

一、前缀和——基本就是公式（容斥原理）

 

 

 一维前缀和数组

将S0定义成0是为了边界处理，统一形式。比如求 [1,10]的前缀和，其实就是S10，但是当我们定义S0 = 0后，我们就依然可以表示为 S10 - S0

#include<iostream>
using namespace std;
const int N  = 100010;
int n,m;
int a[N],b[N];  //原数组和前缀和数组

int main(){
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
    //前缀和数组
    for(int i = 1;i <= n;i ++) b[i] = b[i-1] + a[i];
    while(m--){
        int l,r;
        scanf("%d%d",&l,&r);
        cout<<b[r] - b[l-1]<<endl;
    }
}

 

二维前缀和矩阵

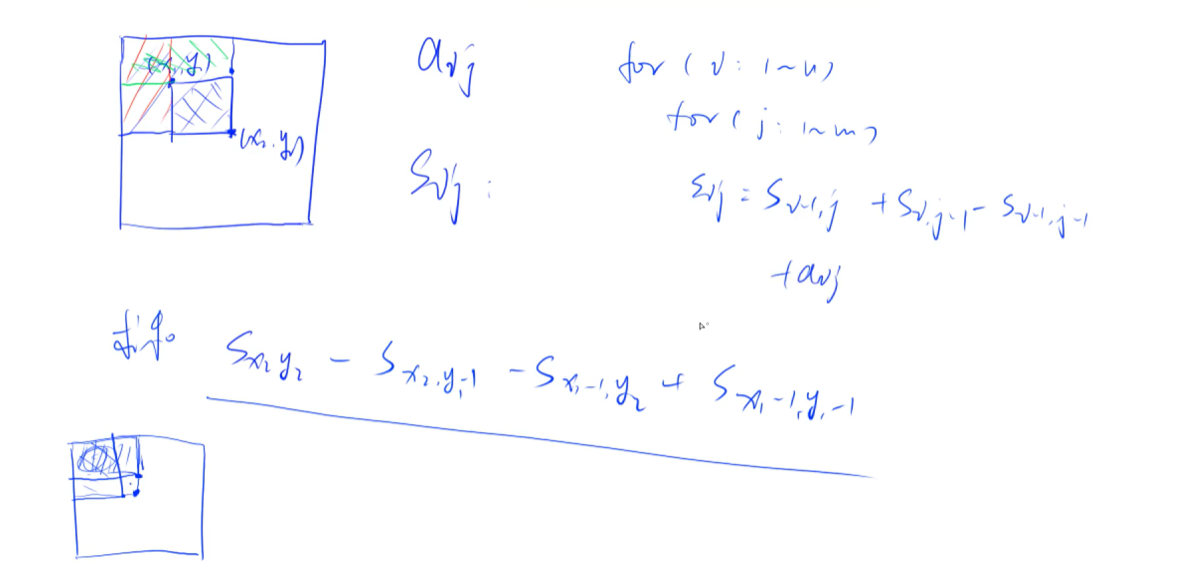
前缀和问题一般是从1开始

#include<iostream>
using namespace std;

const int N = 1010;
int n,m,q;
int a[N][N],b[N][N];

int main(){
    scanf("%d%d%d",&n,&m,&q);
    
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <=m;j++)
            scanf("%d",&a[i][j]);
    
    //前缀和数组
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            b[i][j] =  b[i-1][j] + b[i][j-1] - b[i-1][j-1] + a[i][j];
    while(q--){
        int x1,y1,x2,y2;
        cin>>x1>>y1>>x2>>y2;
        cout<<b[x2][y2] - b[x2][y1 -1] - b[x1 -1][y2] + b[x1-1][y1-1]<<endl;
    }
            
    // for(int i =1;i <= n;i++){
    //     for(int j = 1;j <= m;j++)
    //         printf("%d ",b[i][j]);
    //         puts("");
    // }    
     return 0;   
}

 

　　

 

二、差分

一维差分

题目：https://www.acwing.com/problem/content/799/

其实 a[i] 就是差分数组b[1]...b[ i ][的前缀和

下面使构造方式，简单一看（不用管）

 

#include<iostream>
using namespace std;

const int N = 100010;
int n,m;
int a[N],b[N];  //y原数组和差分数组

//指定区间[l,r]加c,只需要使b[l] +c ,b[r+1] -c即可
void insert(int l,int r,int c){
    b[l] += c;
    b[r+1] -= c;
}

int main(){
    scanf("%d%d",&n,&m);
    
    for(int i = 1;i <= n;i++) scanf("%d",&a[i]); 
    
    for(int i = 1;i <= n;i++) insert(i,i,a[i]);  //做原数组的差分数组
    
    while(m--){
        int l,r,c;
        scanf("%d%d%d",&l,&r,&c);
        insert(l,r,c);
    }
    
    for(int i = 1;i <= n;i ++) b[i] += b[i-1];   //求前缀和
    for(int i = 1;i <= n;i ++) printf("%d ",b[i]);
    
    return 0;
}

开始时不需要考虑如何构造，将其看为0，然后再插一遍就可以了

 

 

二维差分矩阵

题目https://www.acwing.com/problem/content/800/

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

其中 b[i][j]是提前假定好的，性质就是构造b,使得h二维数组a是二维数组b的前缀和

 

#include<iostream>
using namespace std;

const int N = 1010;
int n,m,q;

int a[N][N],b[N][N];  //存放原矩阵和差分矩阵

void insert(int x1,int y1,int x2,int y2,int c){
    b[x1][y1] += c;
    b[x1][y2+1] -= c;
    b[x2+1][y1] -= c;
    b[x2+1][y2+1] += c;
}

int main(){
    scanf("%d%d%d",&n,&m,&q);
    
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            scanf("%d",&a[i][j]);
            
    for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
            insert(i,j,i,j,a[i][j]);
            
    while(q--){
        int x1,y1,x2,y2,c;
        cin>>x1>>y1>>x2>>y2>>c;
        insert(x1,y1,x2,y2,c);
    }
    
    //求前缀和
    for(int i = 1;i <= n;i++){
        for(int j = 1;j <= m;j++){
            b[i][j] += b[i-1][j] + b[i][j-1] -b[i-1][j-1];
            printf("%d ",b[i][j]);
        }   
        cout<<endl;
    }
    
    return 0;
}

 感谢y总！