题目:
Fishnet
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 1604 | Accepted: 1026 |
Description
A fisherman named Etadokah awoke in a very small island. He could see calm, beautiful and blue sea around the island. The previous night he had encountered a terrible storm and had reached this uninhabited island. Some wrecks of his ship were spread around
him. He found a square wood-frame and a long thread among the wrecks. He had to survive in this island until someone came and saved him.
In order to catch fish, he began to make a kind of fishnet by cutting the long thread into short threads and fixing them at pegs on the square wood-frame. He wanted to know the sizes of the meshes of the fishnet to see whether he could catch small fish as well as large ones.
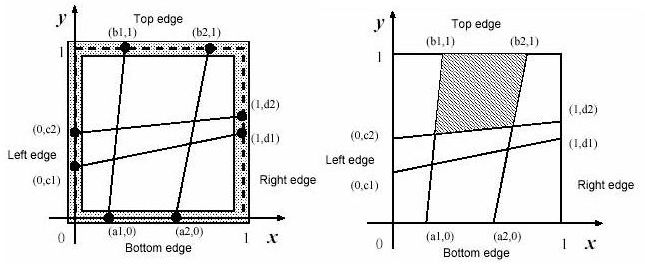
The wood frame is perfectly square with four thin edges on meter long: a bottom edge, a top edge, a left edge, and a right edge. There are n pegs on each edge, and thus there are 4n pegs in total. The positions of pegs are represented by their (x,y)-coordinates. Those of an example case with n=2 are depicted in figures below. The position of the ith peg on the bottom edge is represented by (ai,0). That on the top edge, on the left edge and on the right edge are represented by (bi,1), (0,ci) and (1,di), respectively. The long thread is cut into 2n threads with appropriate lengths. The threads are strained between (ai,0) and (bi,1),and between (0,ci) and (1,di) (i=1,...,n).
You should write a program that reports the size of the largest mesh among the (n+1)2 meshes of the fishnet made by fixing the threads at the pegs. You may assume that the thread he found is long enough to make the fishnet and the wood-frame is thin enough for neglecting its thickness.
In order to catch fish, he began to make a kind of fishnet by cutting the long thread into short threads and fixing them at pegs on the square wood-frame. He wanted to know the sizes of the meshes of the fishnet to see whether he could catch small fish as well as large ones.
The wood frame is perfectly square with four thin edges on meter long: a bottom edge, a top edge, a left edge, and a right edge. There are n pegs on each edge, and thus there are 4n pegs in total. The positions of pegs are represented by their (x,y)-coordinates. Those of an example case with n=2 are depicted in figures below. The position of the ith peg on the bottom edge is represented by (ai,0). That on the top edge, on the left edge and on the right edge are represented by (bi,1), (0,ci) and (1,di), respectively. The long thread is cut into 2n threads with appropriate lengths. The threads are strained between (ai,0) and (bi,1),and between (0,ci) and (1,di) (i=1,...,n).
You should write a program that reports the size of the largest mesh among the (n+1)2 meshes of the fishnet made by fixing the threads at the pegs. You may assume that the thread he found is long enough to make the fishnet and the wood-frame is thin enough for neglecting its thickness.

Input
The input consists of multiple sub-problems followed by a line containing a zero that indicates the end of input. Each sub-problem is given in the following format.
n
a1 a2 ... an
b1 b2 ... bn
c1 c2 ... cn
d1 d2 ... dn
you may assume 0 < n <= 30, 0 < ai,bi,ci,di < 1
n
a1 a2 ... an
b1 b2 ... bn
c1 c2 ... cn
d1 d2 ... dn
you may assume 0 < n <= 30, 0 < ai,bi,ci,di < 1
Output
For each sub-problem, the size of the largest mesh should be printed followed by a new line. Each value should be represented by 6 digits after the decimal point, and it may not have an error greater than 0.000001.
Sample Input
2 0.2000000 0.6000000 0.3000000 0.8000000 0.1000000 0.5000000 0.5000000 0.6000000 2 0.3333330 0.6666670 0.3333330 0.6666670 0.3333330 0.6666670 0.3333330 0.6666670 4 0.2000000 0.4000000 0.6000000 0.8000000 0.1000000 0.5000000 0.6000000 0.9000000 0.2000000 0.4000000 0.6000000 0.8000000 0.1000000 0.5000000 0.6000000 0.9000000 2 0.5138701 0.9476283 0.1717362 0.1757412 0.3086521 0.7022313 0.2264312 0.5345343 1 0.4000000 0.6000000 0.3000000 0.5000000 0
Sample Output
0.215657 0.111112 0.078923 0.279223 0.348958
Source
题意:
求最大四边形面积
注意:
点的输入顺序【周边上点,都是按照从小到大的顺序输入的】
算法: 枚举+线段求交点+叉积求面积
思路:
存储每一个点【周边的+线段交点】,
然后依次遍历每一个四边形的面积
Code:
/****************************************************************************
C Accepted 208 KB 16 ms C++ 2155 B
题意:
在直角坐标系中,把第一象限的那个单位面积的正方形分成 n*n 个小四边形,
求最大四边形面积
注意:点的输入顺序【周边上点,都是按照从小到大的顺序输入的】
算法:枚举+线段求交点+叉积求面积
思路:存储每一个点【周边的+交点】,
然后依次遍历每一个四边形的面积
******************************************************************************/
#include<stdio.h>
#include<math.h>
#include<algorithm>
using namespace std;
const int maxn = 40;
struct Point{
double x,y;
Point() {}
Point(double _x, double _y){
x = _x;
y = _y;
}
Point operator + (const Point &B) const {
return Point(x+B.x, y+B.y);
}
Point operator - (const Point &B) const {
return Point(x-B.x, y-B.y);
}
Point operator * (const double &p) const {
return Point(p*x, p*y);
}
}p[maxn][maxn];
typedef Point Vector;
/** 叉积求面积 */
double Cross(Point A, Point B)
{
return A.x*B.y - A.y*B.x;
}
/** 求线段交点 */
Point GetLineIntersection(Point P, Vector v, Point Q, Vector w){
Vector u = P-Q;
double t = Cross(w, u) / Cross(v, w);
return P+v*t;
}
/** 根据四个点用叉积求四边形面积 */
double Area(Point a, Point b, Point c, Point d){
return fabs(Cross(c-a,b-a)) / 2.0 + fabs(Cross(c-a,d-a)) / 2.0;
}
int main()
{
int n;
while(scanf("%d", &n) != EOF)
{
if(n == 0) break;
p[0][0] = Point(0,1); //定位四个顶点
p[0][n+1] = Point(1,1);
p[n+1][0] = Point(0,0);
p[n+1][n+1] = Point(1,0);
double a,b,c,d; //依次存储周边的点
for(int i = 1; i <= n; i++) //a
{
scanf("%lf", &a);
p[n+1][i] = Point(a,0);
}
for(int i = 1; i <= n; i++)// b
{
scanf("%lf", &b);
p[0][i] = Point(b,1);
}
for(int i = n; i >= 1; i--) //c
{
scanf("%lf", &c);
p[i][0] = Point(0,c);
}
for(int i = n; i >= 1; i--) //d
{
scanf("%lf", &d);
p[i][n+1] = Point(1,d);
}
//求中间的交点
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
p[i][j] = GetLineIntersection(p[i][0], p[i][0]-p[i][n+1], p[n+1][j], p[n+1][j]-p[0][j]);
}
}
double ans = 0;
double tmp;
//从上到下、从左到右依次遍历每个四边形
for(int i = 0; i <= n; i++)
{
for(int j = 0; j <= n; j++)
{
tmp = Area(p[i][j],p[i][j+1],p[i+1][j+1],p[i+1][j]);
ans = max(ans,tmp);
}
}
printf("%.6lf
", ans);
}
return 0;
}
PS:很简单基础的一道计算几何了,昨天却纠结了很久都没有弄出样例,感觉自己写程序的心态还是很不好,过于心浮气躁,今天早上电脑什么也没开,打开网页和 cb 就直接敲这题,敲了大概半个小时【写程序的速度还是太慢了】,最后总算是一气呵成,1A 了。暑假过了一半了却还没什么进步,acm 生涯也可能就只有这几个月了,而下个月又是最关键的月,加油吧!!!Just do it