浅析Golang map的实现原理

Golang中的map底层使用的数据结构是hash table，基本原理就和基础的散列表一致，重点是Golang在设计中采用了分桶(Bucket)，每个桶里面支持多个key-value元素的这种思路，具体可以参考下面的图[图片来源¹]：

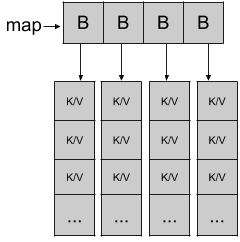
可以看到上面的B就是Bucket，每个桶中会存储多组K/V，map的具体实现在Go源码中src/runtime/map.go²实现，源文件的头部已经对实现做了比较详细的解释，默认情况下map首先是指向一个桶的数组，每个桶中最多包含8个key-value对，对于输入的key首先经过散列函数计算得出散列值，其实就是1个数字，大部分计算机都是64位的，所以通常这是一个uint64的值，这个哈希值的低位用于选择桶，确定桶之后，哈希值的高位用于定位到桶中的条目，如果桶中的key-value满了，则会标记当前桶溢出同时链接到额外的新桶，将元素放进去。

在map的源码实现中，map底层是一个hmap的结构体：

注意到其中有一个元素B，这个B就表示要使用哈希值的低位的位数，用来计算对应的桶，比如使用低8位，那么这里B就等于8，那么桶的个数就是2的8次方，也就是256个桶，这样直接通过与运算就可以将插入的元素定位到桶中去：

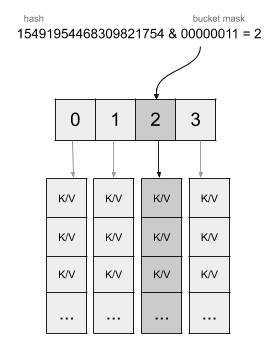
看上面这个图就一目了然了，在4个桶的情况下，直接用64为哈希值和桶的掩码做与运算，也就是取低2位的数值，直接作为桶数组的下标在O(1)的情况下定位到桶。

然后可以看下每个桶中的元素是怎么存的，每个桶是由bmap结构体来表示：

可以看到这里面有个tophash属性，是一个uint8的数组，其中bucketCnt的值在源代码最上面有定义，大小为8，也就是每个桶中可以放8个元素，这里uint8仅仅存放hash值的高8位，可以参考下面这个图：

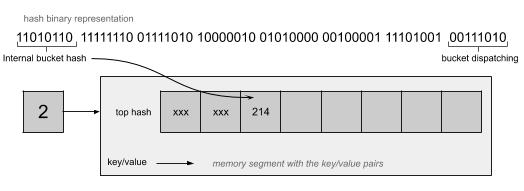
如果两个不同的key被定位到同一个桶中，其实就可以认为出现了哈希冲突，那么这种情况下就依次按照顺序从前往后将hash值的高8位写入到数组空闲的元素中，这里思路和链表法是一致的，之所以这么设计是为了提高哈希冲突时比较的速度，因为比较1个字节要比比较一个很长的key快，这时查找key的过程是先通过计算得到的哈希值定位到桶，然后依次遍历tophash和计算hash值的高8位是否相等，如果相等则说明元素大概率是找到了，这个时候再详细比较key是否完全一致即可，否则将继续寻找，直到找到最后一个元素为止，如果都找不到说明要查找的key是不存在的，如果当前桶存储满了，则会继续挂上新的存储桶，也叫溢出桶，通过这种方式来进行扩展：

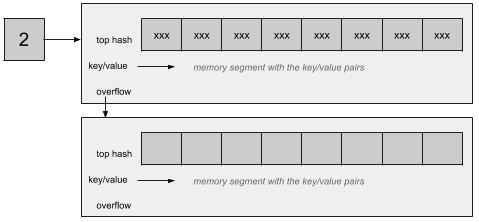
这里每个bmap中存在一个overflow指针指向下一个Bucket，和之前一样继续向后存储冲突的key/value，但是随着桶的增多，搜索元素的速度也会下降，所以不会无限的增加桶，而是会在满足某些条件的情况下进行扩容，具体在每个桶中完整的key和value都是连续存储的，类似于下面这样：

这样存储相比key-value-key-value...的存储方式好处就是可以避免内存填充对齐，从而减少空间的占用，所以上面我们看到的bmap结构体在运行时实际的结构是下面这样的：

type bmap struct {
  topbits  [8]uint8
  keys     [8]keytype
  values   [8]valuetype
  pad      uintptr
  overflow uintptr
}

其中keys和values以数组方式分别进行key和value的连续存储。

然后可以再简单看下扩容，说到扩容在普通散列表中会有装载因子的概念，即实际的元素数量/总的数组长度，当装载因子不断增大时，发生哈希冲突的可能性也会越大，所以这个时候就需要进行扩容操作，装载因子的范围通常在0_{1之间，同样在Go的map中也有装载因子的概念，只是定义略有不同，这里装载因子=元素个数/Bucket个数=元素个数/2^B，最理想的情况下是每个桶中只有1个元素，这样查找的复杂度是O(1)，但是会带来很大的空间浪费，空间利用率最好的情况是每个桶中都装满8个元素甚至会有比较多的溢出桶，但是这样查找的效率会降低，所以需要寻找一个折中的负载因子阈值，对map进行扩容，可以看到在Go中装载因子很容易就大于1，通常在1}8之间，实际上默认的装载因子阈值为6.5，也就是说比较良好的情况下，平均每个桶中的元素不超过6.5个，是空间和时间上比较好的平衡，在源码中可以看到扩容因子的定义：

那么具体的扩容时机是什么样的呢？在插入函数的源码中有对应的逻辑：

可以看出当满足overLoadFactor或tooManyOverflowBuckets的情况下，且当前没有在扩容状态时，则开始执行扩容，具体overLoadFactor和tooManyOverflowBuckets的代码如下：

这两段代码其实都比较简单，overLoadFactor其实就是说当前的元素总数比较多，负载因子已经超过扩容因子6.5时，会进行扩容操作，具体的细节可以再看bucketShift函数：

这里b传入的就是B，也就是低位的位数，这里goarch.PtrSize具体在internal/goarch/goarch.go中定义如下：

所以在32位系统上就是，64位系统上就是8，所以上面就是B和63进行与运算，正常B是不可能超过63的，所以bucketShift的返回值也就是2^B，判断的条件就变为：count > 13*(2^B/2)，也就是元素个数大于桶个数*6.5时，会触发扩容。

另外的tooManyOverflowBuckets看字面意思就是当溢出桶比较多时，也会出发扩容，具体的就是noverflow大于2^{B时，也就是溢出桶的个数超过原始桶的个数时说明溢出桶非常多了，开始触发扩容，当然B大于15时也是按15算，也就是说溢出桶永远不能超过2}15也就是32768个。

上面就简单说了一下扩容的操作，当然扩容也采用了渐进式的方式进行搬迁，而不是全量进行迁移，可以避免程序的阻塞，也就是说当执行插入、删除等操作时都会尝试进行搬迁操作，查看扩容操作可以发现，当分配新的bucket后，只是将老的bucket挂到新的oldbuckets指针上，并没有真正的进行迁移。

根据上面的扩容原理，如果我们能提前预知到元素的数量可以在分配map时指定元素的个数，从而避免扩容操作，Go在makemap时，指定的大小时Bucket的个数，当我们的元素数量比较多的时候，为了节省空间，不需要分配这么多Bucket，总体上保证在扩容因子之下即可，所以假如我们有10万个元素我们可以按照下面的方式分配：

// 分配元素个数/6或者元素个数/5，使负载因子占用始终在扩容阈值之下
m := make(map[uint64]string, 100000/6)

按照上面的方式分配可以使负载因子占用始终在扩容阈值之下，从而尽量的避免扩容带来的开销，当然如果哈希分布不均匀，也有可能出现溢出桶过多而扩容的情况，不过通常情况下分布还是较为均匀的，这样可以节省很多的空间。

另外map的遍历时按照Bucket的顺序遍历，每个Bucket按照内部的数组顺序遍历，所以很容易理解其实是无序的。

根据上面的hmap和bmap定义也可以知道，实际的map占用的空间可以按照下面的公式计算：

// 这里没有考虑扩容时的备用桶、溢出桶以及内存对齐等占用
unsafe.Sizeof(hmap) + len(map)*8*(unsafe.Sizeof(key)+unsafe.Sizeof(value))

如果时内存要求比较严格的情况下，例如value尽量用数字类型，如果是切片类型可以用切片指针来引用，因为指针长度是8字节，而切片引用是24个字节，而如果是结构体类型尽量用结构体指针来引用，因为Go中结构体为值拷贝占用的空间会比较大，所以无论是切片还是结构体随着元素个数增多消耗会更明显，所以类型这块要做好设计。

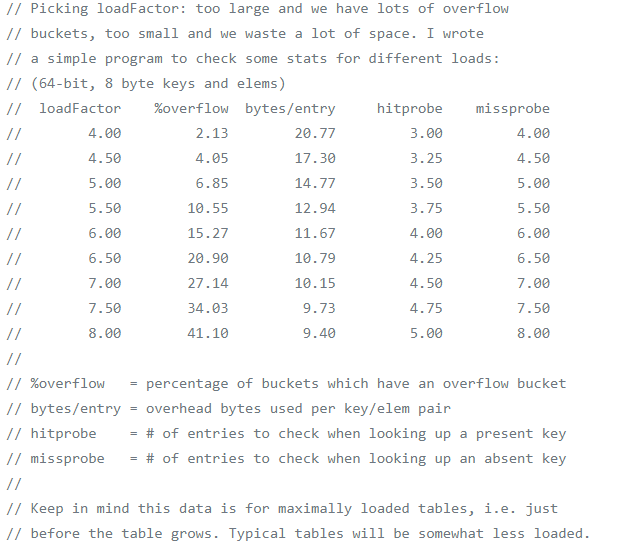
最后就是源码中设定不同的负载因子所进行的一些统计如下：

reference

1.部分图片及内容参考

2.map源码