转载请注明出处： http://www.cnblogs.com/fraud/ ——by fraud
Scrooge McDuck keeps his most treasured savings in a home safe with a combination lock. Each time he wants to put there the treasures that he's earned fair and square, he has to open the lock.
The combination lock is represented by n rotating disks with digits from 0 to 9 written on them. Scrooge McDuck has to turn some disks so that the combination of digits on the disks forms a secret combination. In one move, he can rotate one disk one digit forwards or backwards. In particular, in one move he can go from digit 0 to digit 9 and vice versa. What minimum number of actions does he need for that?
The first line contains a single integer n (1 ≤ n ≤ 1000) — the number of disks on the combination lock.
The second line contains a string of n digits — the original state of the disks.
The third line contains a string of n digits — Scrooge McDuck's combination that opens the lock.
Print a single integer — the minimum number of moves Scrooge McDuck needs to open the lock.
5
82195
64723
13
In the sample he needs 13 moves:
- 1 disk:
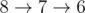
- 2 disk:
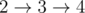
- 3 disk:
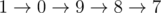
- 4 disk:
- 5 disk:
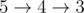
1 #include <iostream> 2 #include <sstream> 3 #include <ios> 4 #include <iomanip> 5 #include <functional> 6 #include <algorithm> 7 #include <vector> 8 #include <string> 9 #include <list> 10 #include <queue> 11 #include <deque> 12 #include <stack> 13 #include <set> 14 #include <map> 15 #include <cstdio> 16 #include <cstdlib> 17 #include <cmath> 18 #include <cstring> 19 #include <climits> 20 #include <cctype> 21 using namespace std; 22 #define XINF INT_MAX 23 #define INF 0x3FFFFFFF 24 #define MP(X,Y) make_pair(X,Y) 25 #define PB(X) push_back(X) 26 #define REP(X,N) for(int X=0;X<N;X++) 27 #define REP2(X,L,R) for(int X=L;X<=R;X++) 28 #define DEP(X,R,L) for(int X=R;X>=L;X--) 29 #define CLR(A,X) memset(A,X,sizeof(A)) 30 #define IT iterator 31 typedef long long ll; 32 typedef pair<int,int> PII; 33 typedef vector<PII> VII; 34 typedef vector<int> VI; 35 string s1,s2; 36 int main() 37 { 38 ios::sync_with_stdio(false); 39 int n; 40 cin>>n; 41 cin>>s1>>s2; 42 int ans=0; 43 for(int i=0;i<n;i++){ 44 int l=s1[i]-'0'; 45 int r=s2[i]-'0'; 46 ans+=min(abs((l+10)-r),min(abs(l-(r+10)),abs(l-r))); 47 } 48 cout<<ans<<endl;; 49 return 0; 50 }
Little Vova studies programming in an elite school. Vova and his classmates are supposed to write n progress tests, for each test they will get a mark from 1 to p. Vova is very smart and he can write every test for any mark, but he doesn't want to stand out from the crowd too much. If the sum of his marks for all tests exceeds value x, then his classmates notice how smart he is and start distracting him asking to let them copy his homework. And if the median of his marks will be lower than y points (the definition of a median is given in the notes), then his mom will decide that he gets too many bad marks and forbid him to play computer games.
Vova has already wrote k tests and got marks a1, ..., ak. He doesn't want to get into the first or the second situation described above and now he needs to determine which marks he needs to get for the remaining tests. Help him do that.
The first line contains 5 space-separated integers: n, k, p, x and y (1 ≤ n ≤ 999, n is odd, 0 ≤ k < n, 1 ≤ p ≤ 1000, n ≤ x ≤ n·p, 1 ≤ y ≤ p). Here n is the number of tests that Vova is planned to write, k is the number of tests he has already written, p is the maximum possible mark for a test, x is the maximum total number of points so that the classmates don't yet disturb Vova, y is the minimum median point so that mom still lets him play computer games.
The second line contains k space-separated integers: a1, ..., ak (1 ≤ ai ≤ p) — the marks that Vova got for the tests he has already written.
If Vova cannot achieve the desired result, print "-1".
Otherwise, print n - k space-separated integers — the marks that Vova should get for the remaining tests. If there are multiple possible solutions, print any of them.
5 3 5 18 4
3 5 4
4 1
5 3 5 16 4
5 5 5
-1
The median of sequence a1, ..., an where n is odd (in this problem n is always odd) is the element staying on (n + 1) / 2 position in the sorted list of ai.
In the first sample the sum of marks equals 3 + 5 + 4 + 4 + 1 = 17, what doesn't exceed 18, that means that Vova won't be disturbed by his classmates. And the median point of the sequence {1, 3, 4, 4, 5} equals to 4, that isn't less than 4, so his mom lets him play computer games.
Please note that you do not have to maximize the sum of marks or the median mark. Any of the answers: "4 2", "2 4", "5 1", "1 5", "4 1", "1 4" for the first test is correct.
In the second sample Vova got three '5' marks, so even if he gets two '1' marks, the sum of marks will be 17, that is more than the required value of 16. So, the answer to this test is "-1".
1 #include <iostream> 2 #include <sstream> 3 #include <ios> 4 #include <iomanip> 5 #include <functional> 6 #include <algorithm> 7 #include <vector> 8 #include <string> 9 #include <list> 10 #include <queue> 11 #include <deque> 12 #include <stack> 13 #include <set> 14 #include <map> 15 #include <cstdio> 16 #include <cstdlib> 17 #include <cmath> 18 #include <cstring> 19 #include <climits> 20 #include <cctype> 21 using namespace std; 22 #define XINF INT_MAX 23 #define INF 0x3FFFFFFF 24 #define MP(X,Y) make_pair(X,Y) 25 #define PB(X) push_back(X) 26 #define REP(X,N) for(int X=0;X<N;X++) 27 #define REP2(X,L,R) for(int X=L;X<=R;X++) 28 #define DEP(X,R,L) for(int X=R;X>=L;X--) 29 #define CLR(A,X) memset(A,X,sizeof(A)) 30 #define IT iterator 31 typedef long long ll; 32 typedef pair<int,int> PII; 33 typedef vector<PII> VII; 34 typedef vector<int> VI; 35 int a[10010]; 36 int main() 37 { 38 ios::sync_with_stdio(false); 39 int n,k,p,x,y; 40 int temp =0; 41 cin>>n>>k>>p>>x>>y; 42 for(int i=0;i<k;i++){ 43 cin>>a[i]; 44 temp +=a[i]; 45 } 46 sort(a,a+k); 47 int m= lower_bound(a,a+k,y)-a; 48 int cha = n/2; 49 if(m>cha){ 50 cout<<"-1"<<endl; 51 return 0; 52 } 53 int gao1=min(cha - m,n-k); 54 int gao2=n-k-gao1; 55 if(temp+gao1+y*gao2>x){ 56 cout<<"-1"<<endl; 57 return 0; 58 } 59 for(int i=0;i<gao1;i++){ 60 cout<<1<<" "; 61 } 62 for(int i=0;i<gao2;i++){ 63 cout<<y<<" "; 64 } 65 cout<<endl; 66 return 0; 67 }
You play a computer game. Your character stands on some level of a multilevel ice cave. In order to move on forward, you need to descend one level lower and the only way to do this is to fall through the ice.
The level of the cave where you are is a rectangular square grid of n rows and m columns. Each cell consists either from intact or from cracked ice. From each cell you can move to cells that are side-adjacent with yours (due to some limitations of the game engine you cannot make jumps on the same place, i.e. jump from a cell to itself). If you move to the cell with cracked ice, then your character falls down through it and if you move to the cell with intact ice, then the ice on this cell becomes cracked.
Let's number the rows with integers from 1 to n from top to bottom and the columns with integers from 1 to m from left to right. Let's denote a cell on the intersection of the r-th row and the c-th column as (r, c).
You are staying in the cell (r1, c1) and this cell is cracked because you've just fallen here from a higher level. You need to fall down through the cell (r2, c2) since the exit to the next level is there. Can you do this?
The first line contains two integers, n and m (1 ≤ n, m ≤ 500) — the number of rows and columns in the cave description.
Each of the next n lines describes the initial state of the level of the cave, each line consists of m characters "." (that is, intact ice) and "X" (cracked ice).
The next line contains two integers, r1 and c1 (1 ≤ r1 ≤ n, 1 ≤ c1 ≤ m) — your initial coordinates. It is guaranteed that the description of the cave contains character 'X' in cell (r1, c1), that is, the ice on the starting cell is initially cracked.
The next line contains two integers r2 and c2 (1 ≤ r2 ≤ n, 1 ≤ c2 ≤ m) — the coordinates of the cell through which you need to fall. The final cell may coincide with the starting one.
If you can reach the destination, print 'YES', otherwise print 'NO'.
4 6
X...XX
...XX.
.X..X.
......
1 6
2 2
YES
5 4
.X..
...X
X.X.
....
.XX.
5 3
1 1
NO
4 7
..X.XX.
.XX..X.
X...X..
X......
2 2
1 6
YES
In the first sample test one possible path is:
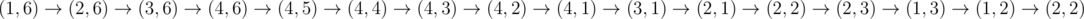
After the first visit of cell (2, 2) the ice on it cracks and when you step there for the second time, your character falls through the ice as intended.
注意判一下是否存在除起点过来的那个方向的点外另外三个方向中有'.'点，即可。
1 #include <iostream> 2 #include <sstream> 3 #include <ios> 4 #include <iomanip> 5 #include <functional> 6 #include <algorithm> 7 #include <vector> 8 #include <string> 9 #include <list> 10 #include <queue> 11 #include <deque> 12 #include <stack> 13 #include <set> 14 #include <map> 15 #include <cstdio> 16 #include <cstdlib> 17 #include <cmath> 18 #include <cstring> 19 #include <climits> 20 #include <cctype> 21 using namespace std; 22 #define XINF INT_MAX 23 #define INF 0x3FFFFFFF 24 #define MP(X,Y) make_pair(X,Y) 25 #define PB(X) push_back(X) 26 #define REP(X,N) for(int X=0;X<N;X++) 27 #define REP2(X,L,R) for(int X=L;X<=R;X++) 28 #define DEP(X,R,L) for(int X=R;X>=L;X--) 29 #define CLR(A,X) memset(A,X,sizeof(A)) 30 #define IT iterator 31 typedef long long ll; 32 typedef pair<int,int> PII; 33 typedef vector<PII> VII; 34 typedef vector<int> VI; 35 char a[510][510]; 36 int b[510][510]; 37 int dirx[4]={-1,0,0,1}; 38 int diry[4]={0,1,-1,0}; 39 int n,m; 40 bool vis[510][510]; 41 bool in(int x,int y){ 42 if(x>=0&&x<n&&y>=0&&y<m&&b[x][y])return 1; 43 return 0; 44 } 45 int main() 46 { 47 ios::sync_with_stdio(false); 48 49 cin>>n>>m; 50 for(int i=0;i<n;i++){ 51 for(int j=0;j<m;j++){ 52 cin>>a[i][j]; 53 if(a[i][j]=='X')b[i][j]=0; 54 else b[i][j]=1; 55 } 56 } 57 int sx,sy; 58 int gx,gy; 59 cin>>sx>>sy; 60 cin>>gx>>gy; 61 sx--;sy--; 62 gx--;gy--; 63 int c=0; 64 bool flag=0; 65 queue<PII>q; 66 q.push(MP(sx,sy)); 67 vis[sx][sy]=1; 68 while(!q.empty()){ 69 PII p =q.front(); 70 q.pop(); 71 int dx= p.first; 72 int dy = p.second; 73 for(int i=0;i<4;i++){ 74 int tx=dx+dirx[i]; 75 int ty=dy+diry[i]; 76 if(tx==gx&&ty==gy){ 77 int d=0; 78 for(int j=0;j<4;j++){ 79 if(in(gx+dirx[j],gy+diry[j]))c++; 80 if(vis[gx+dirx[j]][gy+diry[j]]&&in(gx+dirx[j],gy+diry[j]))d=1; 81 } 82 if((((c>1&&d)||(c&&!d))&&b[gx][gy])||!b[gx][gy])cout<<"YES"<<endl; 83 else cout<<"NO"<<endl; 84 return 0; 85 } 86 if(in(tx,ty)&&!vis[tx][ty]){ 87 vis[tx][ty]=1; 88 q.push(MP(tx,ty)); 89 } 90 } 91 } 92 cout<<"NO"<<endl; 93 return 0; 94 }
The Bad Luck Island is inhabited by three kinds of species: r rocks, s scissors and p papers. At some moments of time two random individuals meet (all pairs of individuals can meet equiprobably), and if they belong to different species, then one individual kills the other one: a rock kills scissors, scissors kill paper, and paper kills a rock. Your task is to determine for each species what is the probability that this species will be the only one to inhabit this island after a long enough period of time.
The single line contains three integers r, s and p (1 ≤ r, s, p ≤ 100) — the original number of individuals in the species of rock, scissors and paper, respectively.
Print three space-separated real numbers: the probabilities, at which the rocks, the scissors and the paper will be the only surviving species, respectively. The answer will be considered correct if the relative or absolute error of each number doesn't exceed 10 - 9.
2 2 2
0.333333333333 0.333333333333 0.333333333333
2 1 2
0.150000000000 0.300000000000 0.550000000000
1 1 3
0.057142857143 0.657142857143 0.285714285714
dp[r][s][p]=(r*s*dp[r][s-1][p]+s*p*dp[r][s][p-1]+r*p*dp[r-1][s][p])/(r*s+r*p+s*p)
然后记忆化搜三次即可。
1 #include <iostream> 2 #include <sstream> 3 #include <ios> 4 #include <iomanip> 5 #include <functional> 6 #include <algorithm> 7 #include <vector> 8 #include <string> 9 #include <list> 10 #include <queue> 11 #include <deque> 12 #include <stack> 13 #include <set> 14 #include <map> 15 #include <cstdio> 16 #include <cstdlib> 17 #include <cmath> 18 #include <cstring> 19 #include <climits> 20 #include <cctype> 21 using namespace std; 22 #define XINF INT_MAX 23 #define INF 0x3FFFFFFF 24 #define MP(X,Y) make_pair(X,Y) 25 #define PB(X) push_back(X) 26 #define REP(X,N) for(int X=0;X<N;X++) 27 #define REP2(X,L,R) for(int X=L;X<=R;X++) 28 #define DEP(X,R,L) for(int X=R;X>=L;X--) 29 #define CLR(A,X) memset(A,X,sizeof(A)) 30 #define IT iterator 31 typedef long long ll; 32 typedef pair<int,int> PII; 33 typedef vector<PII> VII; 34 typedef vector<int> VI; 35 double dp[110][110][110]; 36 bool vis[110][110][110]; 37 void dfs(int r,int s,int p){ 38 if((r==0&&s==0)||(r==0&&p==0)||(s==0&&p==0)){ 39 //dp[r][s][p]=1; 40 vis[r][s][p]=1; 41 return; 42 } 43 if(!vis[r-1][s][p]&&r)dfs(r-1,s,p); 44 if(!vis[r][s-1][p]&&s)dfs(r,s-1,p); 45 if(!vis[r][s][p-1]&&p)dfs(r,s,p-1); 46 dp[r][s][p]=(r*s*dp[r][s-1][p]+s*p*dp[r][s][p-1]+r*p*dp[r-1][s][p])/(r*s+s*p+r*p); 47 vis[r][s][p]=1; 48 } 49 int main() 50 { 51 ios::sync_with_stdio(false); 52 int r,s,p; 53 cin>>r>>s>>p; 54 CLR(vis,0); 55 CLR(dp,0); 56 for(int i=0;i<=r;i++){ 57 dp[i][0][0]=1; 58 vis[i][0][0]=1; 59 } 60 dfs(r,s,p); 61 cout<<fixed<<setprecision(12)<<dp[r][s][p]<<" "; 62 CLR(vis,0); 63 CLR(dp,0); 64 for(int i=0;i<=s;i++){ 65 dp[0][i][0]=1; 66 vis[0][i][0]=1; 67 } 68 dfs(r,s,p); 69 cout<<fixed<<setprecision(12)<<dp[r][s][p]<<" "; 70 CLR(vis,0); 71 CLR(dp,0); 72 for(int i=0;i<=p;i++){ 73 dp[0][0][i]=1; 74 vis[0][0][i]=1; 75 } 76 dfs(r,s,p); 77 cout<<fixed<<setprecision(12)<<dp[r][s][p]<<" "; 78 cout<<endl; 79 80 return 0; 81 }
There is an infinite sequence consisting of all positive integers in the increasing order: p = {1, 2, 3, ...}. We performed n swapoperations with this sequence. A swap(a, b) is an operation of swapping the elements of the sequence on positions a and b. Your task is to find the number of inversions in the resulting sequence, i.e. the number of such index pairs (i, j), that i < j and pi > pj.
The first line contains a single integer n (1 ≤ n ≤ 105) — the number of swap operations applied to the sequence.
Each of the next n lines contains two integers ai and bi (1 ≤ ai, bi ≤ 109, ai ≠ bi) — the arguments of the swap operation.
Print a single integer — the number of inversions in the resulting sequence.
2
4 2
1 4
4
3
1 6
3 4
2 5
15
In the first sample the sequence is being modified as follows: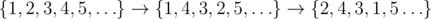 
. It has 4 inversions formed by index pairs (1, 4), (2, 3), (2, 4) and (3, 4).
水题。逆序对必定由两个部分组成：
1.交换过的点和未交换过的点产生。
2.交换过的点和交换过的点。
对于第一种：
对于交换过的数，看它最后所在的位置，和它原来的位置差了几个，然后去掉这个区间内有过交换的数的个数。
对于第二种：
离散化，然后就相当于一个1到k的排列。。。直接树状数组求逆序对
1 #include <iostream> 2 #include <sstream> 3 #include <ios> 4 #include <iomanip> 5 #include <functional> 6 #include <algorithm> 7 #include <vector> 8 #include <string> 9 #include <list> 10 #include <queue> 11 #include <deque> 12 #include <stack> 13 #include <set> 14 #include <map> 15 #include <cstdio> 16 #include <cstdlib> 17 #include <cmath> 18 #include <cstring> 19 #include <climits> 20 #include <cctype> 21 using namespace std; 22 #define XINF INT_MAX 23 #define INF 0x3FFFFFFF 24 #define MP(X,Y) make_pair(X,Y) 25 #define PB(X) push_back(X) 26 #define REP(X,N) for(int X=0;X<N;X++) 27 #define REP2(X,L,R) for(int X=L;X<=R;X++) 28 #define DEP(X,R,L) for(int X=R;X>=L;X--) 29 #define CLR(A,X) memset(A,X,sizeof(A)) 30 #define IT iterator 31 typedef long long ll; 32 typedef pair<int,int> PII; 33 typedef vector<PII> VII; 34 typedef vector<int> VI; 35 map<int,int>ms; 36 int c[500010]; 37 int d[500010]; 38 ll bit[500010],j; 39 map<int,int>m; 40 ll sum(int i){ 41 ll s=0; 42 while(i>0){ 43 s+=bit[i]; 44 i-=i&-i; 45 } 46 return s; 47 } 48 void add(int i,ll x){ 49 while(i<=j){ 50 bit[i]+=x; 51 i+=i&-i; 52 } 53 } 54 int main() 55 { 56 ios::sync_with_stdio(false); 57 int n; 58 cin>>n; 59 int a,b; 60 for(int i=0;i<n;i++){ 61 cin>>a>>b; 62 if(!ms.count(a)&&!ms.count(b)){ 63 ms[a]=b; 64 ms[b]=a; 65 } 66 else if(ms.count(a)&&!ms.count(b)){ 67 ms[b]=ms[a]; 68 ms[a]=b; 69 } 70 else if(!ms.count(a)&&ms.count(b)){ 71 ms[a]=ms[b]; 72 ms[b]=a; 73 }else{ 74 swap(ms[a],ms[b]); 75 } 76 } 77 ll ans=0; 78 for(map<int,int>::iterator it=ms.begin();it!=ms.end();it++){ 79 c[j]=it->first; 80 d[j++]=it->second; 81 } 82 sort(c,c+j); 83 for(int i=0;i<j;i++){ 84 m[c[i]]=i+1; 85 } 86 for(int i=0;i<j;i++){ 87 if(ms[c[i]]>c[i]){ 88 int tx = m[ms[c[i]]]-m[c[i]]; 89 ans+=ms[c[i]]-c[i]-tx; 90 }else if(ms[c[i]]<c[i]){ 91 int tx= m[c[i]]-m[ms[c[i]]]; 92 ans+=c[i]-ms[c[i]]-tx; 93 } 94 } 95 for(int i=0;i<j;i++){ 96 ans+=i-sum(m[d[i]]); 97 add(m[d[i]],1); 98 } 99 cout<<ans<<endl; 100 101 return 0; 102 }