先来介绍一下线段树。
线段树是一个把线段,或者说一个区间储存在二叉树中。如图所示的就是一棵线段树,它维护一个区间的和。
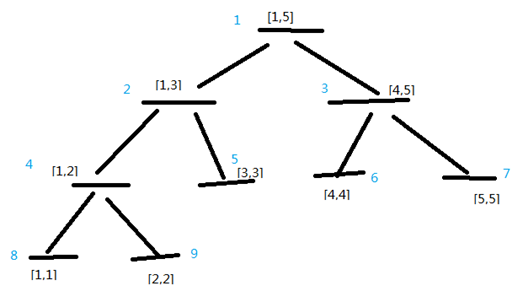
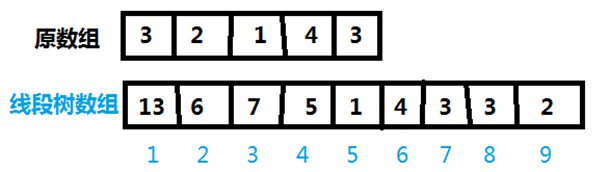
蓝色数字的是线段树的节点在数组中的位置,它表示的区间已经在图上标出,它的值就是这段区间的和。
比如说线段树1号节点表示[1,5]区间,它的值是13,也就是原数组1号位到5号位所有数字加起来的和。
不难发现线段树的下标有这样的性质:
1. 设一个节点的下号是o,那么它的左子树是o*2,右子树是o*2+1。
2. 线段树的大小是原数组的大小*2-1。
3. 线段树叶节点表示区间的长度为1,也就是一个数字,此时区间的左边界=区间的右边界。
但是我们实际使用的时候,线段树是用一个长度为原数组大小4倍的数组储存的,因为方便处理,防止访问叶节点时下标越界。
它支持几种操作:
1. 修改一个点的值
2. 将一个区间加上或减去某个数
3. 查询一个区间的和(乘积也可以),最大/最小值
4. 将一个区间值改变成某个大于0的数
以上时间复杂度都是logn。
建立线段树:
这里我采用递归的方式。在函数内设3个参数,这个线段树节点的下标o,它表示的左区间L,又区间R。从根节点开始递归,如果L=R,就是走到了叶节点(根据性质3),那么该点就是原数组第L(或R)位的值,否则分成两个区间,递归它的左右子树。
代码如下:
1 void init(int o,int L,int R) 2 { 3 if(L==R) sumv[o]=A[L]; //A[]是原数组,sumv[]是线段树数组 4 else 5 { 6 int M=(L+R)/2; 7 init(o*2,L,M); 8 init(o*2+1,M+1,R); 9 sumv[o]=sumv[o*2]+sumv[o*2+1]; 10 } 11 }
这里的sumv是求和线段树数组,我以这个为例。当然如果是维护区间最大/最小,那么第9行的代码应该是左右子树的最大/最小值。
调用:
init(1,1,n);
// 1,n是总区间。
点修改:
与建树的过程类似,从根节点开始,一直递归到叶节点,然后直接修改,完成之后,更新sumv值就可以了。
如果把修改原数组p号位的值修改为v。
代码:
1 int p,v; 2 3 void update(int o,int L,int R) 4 { 5 if(L==R) sumv[o]=v; 6 else 7 { 8 int M=(L+R)/2; 9 if(p<=M) update(o*2,L,M); else update(o*2+1,M+1,R); 10 sumv[o]=sumv[o*2]+sumv[o*2+1]; 11 } 12 }
调用:
先把p,和v赋值好,然后直接调用即可
p=x,v=y;//x,y是你要赋的值
update(1,1,n);
查询区间的和:
还是与上面类似。从根节点开始递归。如果这一层的区间[L,R]包含于要求的区间[y1,y2],那么就把这一层的值累加,否则就访问它的子树,把这个区间一份为二。
如果它的子树表示的区间与要求的区间有交集,就说明有需要访问,否则就不用。
代码:
1 int y1,y2,ans; 2 void query(int o,int L,int R) 3 { 4 if(y1<=L && R<=y2) ans+=sumv[o]; 5 else 6 { 7 int M=(L+R)/2; 8 if(y1<=M) query(o*2,L,M); 9 if(y2>M) query(o*2+1,M+1,R); 10 } 11 }
调用:
把要查找的区间y1,y2赋值好,并把存储答案的ans清0,,再调用即可
y1=x,y2=y,ans=0;//注意ans一定要初始化,最后查出来的答案是保存在ans里面的。
query(1,1,n);
点修改的说明就到此。
测试的题目:codevs 1080 线段树练习
链接:http://codevs.cn/problem/1080/
附代码:
1 #include<cstdio> 2 #include<iostream> 3 using namespace std; 4 const int maxn=100010; 5 6 int A[maxn],sumv[maxn*4],n,m; 7 8 void init(int o,int L,int R) 9 { 10 if(L==R) sumv[o]=A[L]; 11 else 12 { 13 int M=(L+R)/2; 14 init(o*2,L,M); 15 init(o*2+1,M+1,R); 16 sumv[o]=sumv[o*2]+sumv[o*2+1]; 17 } 18 } 19 20 int p,v; 21 void update(int o,int L,int R) 22 { 23 if(L==R) sumv[o]=v; 24 else 25 { 26 int M=(L+R)/2; 27 if(p<=M) update(o*2,L,M); else update(o*2+1,M+1,R); 28 sumv[o]=sumv[o*2]+sumv[o*2+1]; 29 } 30 } 31 32 int y1,y2,ans; 33 void query(int o,int L,int R) 34 { 35 if(y1<=L && R<=y2) ans+=sumv[o]; 36 else 37 { 38 int M=(L+R)/2; 39 if(y1<=M) query(o*2,L,M); 40 if(y2>M) query(o*2+1,M+1,R); 41 } 42 } 43 44 int main() 45 { 46 cin>>n; 47 for(int i=1;i<=n;i++) cin>>A[i]; 48 init(1,1,n); 49 cin>>m; 50 for(int i=1,k,x,y;i<=m;i++) 51 { 52 cin>>k>>x>>y; 53 if(k==1) 54 { 55 p=x,v=A[p]+y; 56 A[p]=v; 57 update(1,1,n); 58 } 59 else 60 { 61 y1=x,y2=y,ans=0; 62 query(1,1,n); 63 cout<<ans<<endl; 64 } 65 } 66 return 0; 67 }