POJ2676-Sudoku（数独）

想了好久没想到好的解决办法，参考了 http://user.qzone.qq.com/289065406/blog/1303713313

大致题意：

九宫格问题，也有人叫数独问题

把一个9行9列的网格，再细分为9个3*3的子网格，要求每行、每列、每个子网格内都只能使用一次1~9中的一个数字，即每行、每列、每个子网格内都不允许出现相同的数字。

 

0是待填位置，其他均为已填入的数字。

要求填完九宫格并输出（如果有多种结果，则只需输出其中一种）

如果给定的九宫格无法按要求填出来，则输出原来所输入的未填的九宫格

 

解题思路：

DFS试探，失败则回溯

 

用三个数组进行标记每行、每列、每个子网格已用的数字，用于剪枝

bool row[10][10];    //row[i][x]  标记在第i行中数字x是否出现了

bool col[10][10];    //col[j][y]  标记在第j列中数字y是否出现了

bool grid[10][10];   //grid[k][x] 标记在第k个3*3子格中数字z是否出现了

 

row 和 col的标记比较好处理，关键是找出grid子网格的序号与 行i列j的关系

即要知道第i行j列的数字是属于哪个子网格的

 

首先我们假设子网格的序号如下编排：

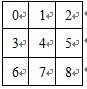
由于1<=i、j<=9，我们有： （其中“/”是C++中对整数的除法）

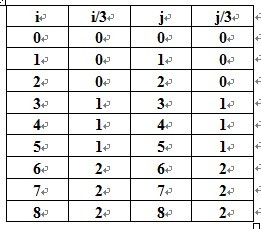
令a= i/3 , b= j/3  ，根据九宫格的 行列 与 子网格 的 关系，我们有:

 

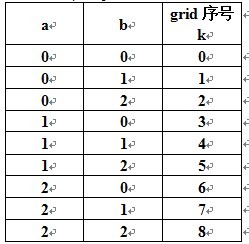
不难发现 3a+b=k

即 3*(i/3)+j/3=k

 

又我在程序中使用的数组下标为 1~9，grid编号也为1~9

因此上面的关系式可变形为 3*((i-1)/3)+(j-1)/3+1=k

 

 

有了这个推导的关系式，问题的处理就变得非常简单了，直接DFS即可

//Memory Time
//216K  422MS

#include<iostream>
using namespace std;
//纵x 行y  即x行y列
int map[10][10]; //九宫格

bool row[10][10];    //row[i][x]  标记在第i行中数字x是否出现了
bool col[10][10];    //col[j][y]  标记在第j列中数字y是否出现了
bool grid[10][10];   //grid[k][x] 标记在第k个3*3子格中数字z是否出现了

							//(这里说明的字母不代表下面程序中的变量)

bool DFS(int x,int y)
{

	//满足的条件是：找到最后一个 如果是true 那回溯上来都会是true 这是成立的情况 如果在中间出现false
	//就要往前回溯 换个数字试试；
	//成功的条件是
	if(x==10)return true;//前面所有都满足了 已经没得找了
	bool flag=false;
	if(map[x][y]){
		//if(x<9)DFS(x+1,y);  //这样找的话会重复
		//else if(y<9)DFS(x,y+1);
		//所以我们一行一行找
		if(y<9)
		flag=	DFS(x,y+1);
		else flag=DFS(x+1,1);
		return flag;//回溯 成功返回TRUE
	}
	else {
		int k=3*((x-1)/3)+(y-1)/3+1;  //k为第几个子方格
		for(int i=1;i<=9;i++)   //枚举数字1~9填空
		{
			if(row[x][i]==false&&col[y][i]==false&&grid[k][i]==false){
								map[x][y]=i;
								row[x][i]=true;
								col[y][i]=true;
								grid[k][i]=true;
								//继续下找
								if(y<9)
										flag	=DFS(x,y+1);
								else flag=DFS(x+1,1);
								if(flag==false){//不满足就原路返回
									map[x][y]=0;
									row[x][i]=false;
									col[y][i]=false;
									grid[k][i]=false;
								}
								else return true;

			}

		}
	}
	return false; //所有数字试过都不行的话
}

int main()
{
	int test;
	int i,j;
	char MAP[10][10];
	cin>>test;
	while(test--)
	{
		/*Initial*/

		memset(row,false,sizeof(row));
		memset(col,false,sizeof(col));
		memset(grid,false,sizeof(grid));
		
		/*Input*/
		for(i=1;i<=9;i++)
			for(j=1;j<=9;j++)
			{
				cin>>MAP[i][j];  //只能输入字符
				map[i][j]=MAP[i][j]-'0';
				if(map[i][j])//记录
				{
					int k=3*((i-1)/3)+(j-1)/3+1;
					row[i][ map[i][j] ]=true;
					col[j][ map[i][j] ]=true;
					grid[k][ map[i][j] ]=true;
				}
			}
		
		/*Fill the Sudoku*/
		DFS(1,1);

		for(i=1;i<=9;i++)
		{
			for(j=1;j<=9;j++)
				cout<<map[i][j];
			cout<<endl;
		}
	}
	return 0;
}

版权声明：本文为博主原创文章，未经博主允许不得转载。